• 1. 与 groth16 的不同
• 2. plonk 中的约束
  • 2.1 门约束
  • 2.2 copy constrains
• 3. 单位根
• 4. 最终证明过程
  • 4.1 符号约定
  • 4.2 要证明什么
  • 4.3 证明过程
    • 4.3.1 提前准备
    • 4.3.2 Round 1
    • 4.3.3 Round 2
    • 4.3.4 Round 3
    • 4.3.5 Round 4
    • 4.3.6 Round 5
  • 4.4 验证过程
  • 4.5 验证的意义
• 5. 总结

前面我们花了很大篇章介绍了一种零知识证明算法：Groth16 。有了这个基础之后，这篇文章我们要学习一种业界更常用的算法：Plonk 。

为什么说 Plonk 在业界更常用呢？因为 Groth16 有一个特点：每次电路变化后，都要重新做一次 trusted setup 。在实践中，这个过程中很慢的，一般项目方要把新的 trusted setup 过程公开出来，然后等待足够多的时间（一个月甚至几个月），让各方进行 setup 。一般情况下没有项目愿意在升级电路时，等待这么长时间。而 Plonk 则不需要这个过程，所以实践中，Plonk 及其涉生的算法被采用得更多一些。

这也不是说 Groth16 在实践中就没有意义。相比于 Plonk ，Groth16 一个非常大的优点是生成 proof 非常快，可能快 10 倍不止。所以如果项目的逻辑很稳定，正式发布后几乎不会再变，就非常适合用 Groth16 ，比如 ZCash 。

不过从文章标题你也看到了，这篇文章只是「囫囵吞枣」地学习 plonk ，因为目前我对 plonk 的一些地方还不是完全理解。随着以后慢慢理解得更深入了，我会补充到这篇文章里，或许最终会把「囫囵吞枣」这个词去掉（但愿吧哈哈）。

1. 与 groth16 的不同

整体来说，plonk 与 groth16 完全不同。

（你不这是逗我玩呢嘛，完全不同还比较个啥）

但完全不同也不是不能比较，我们可以从根源上来了解这两者不一样的地方。

第一个显著的不同是，在 groth16 中，我们把要证明的问题等价转换成了 $L(x) \times R(x) = O(x) + t(x)h(x)$ 这样的形式；但在 Plonk 中，我们则把问题等价转换成 $q_L(x)a(x) + q_R(x)b(x) + q_M(x)a(x)b(x) + q_O(x)c(x) + q_C(x) = 0$ 这样一个多项式等式。

第二个显著的不同是，在 groth16 中，要保证 prover 在计算时对所有的变量多项式（$u_i(x), v_i(x), w_i(x)$）使用了相同的变量（$a_i$），算法要求在 setup 阶段就计算好 $\left{\frac{ {\beta}u_i(x)+{\alpha}v_i(x)+w_i(x)}{\gamma}\right}{i \in [0,..,\mathscr{l}]}$ 和 $\left{\frac{ {\beta}u_i(x)+{\alpha}v_i(x)+w_i(x)}{\delta}\right}{i \in [{\mathscr{l}+1,..m}]}$ 这两项，然后让 prover 直接使用，通过这种方式来保证 witness 使用的一致性；但这种方式有个缺点，就是电路一旦确定了（即 $u_i(x)$ 等这些多项式确定了），setup 里的这些值就不能变了，反过来如果要改更电路，那就得重新做 setup 这个过程，在实际中这个过程还是比较慢的（等给足够的时候让各方对数据进行 setup 加密）。 而在 plonk 中则去掉了这个限制，即更改电路不需要重新 setup 。但 witness 一致性的问题依然存在，既然不能通过 setup 来保证，那 plonk 是怎么解决这个问题的呢？在 plonk 中，有一个 copy constrains 的概念，通过 copy constrains 来限制和保证 witness 的一致性。

2. plonk 中的约束

在 groth16 里，当我们要将一个逻辑运算表达为约束时，使用的是 $L \times R = O$ 这样的方式，其中 $L$ 、$R$ 和 $O$ 里面可以有加法和减法（但不能有乘法）。

比如在 groth16 的文章里的例子里，我们有这样一个函数：

fn foo(w: bool, a: i32, b: i32) -> i32 {
	if w {
		return a * b
	} else {
		return a + b
	}
}

它数学的表达方式是：

令 $y = f(w, a, b)$ ，经过优化后，变成了：

在 groth16 中，我们把上面的数学等式变成约束时，我们得到了以下三条约束：

可以看到在 groth16 中，约束虽然是 $L \times R = O$ 这种形式，但在 $L$ 、$R$ 和 $O$ 中，都允许无数个变量的加法和减法的存在。但在 plonk 中 不能这么干了。在 plonk 中，约束除了乘法，还可以有加法，但不能在 $L$ 、$R$ 和 $O$ 中还有其它运算存在。所以 $w \times (a \times b - a - b) = y - a - b$ 在 plonk 中变成约束等式，应该是：

可以看到，plonk 中的约束相比于 groth16 的约束数量变多了，中间变量也变多了。你可能会问这有什么好处吗？这不是变得更复杂了吗？plonk 这样做，是为了避免在 setup 阶段涉及到电路，从而达到「电路改变不需要重新 setup」的效果。具体原因我们后面会再次提到并详细说明。

但这里有一个很重要的问题：我们如何保证每个约束等式之间使用的是同一个值？比如如何保证第一个约束里的 $a$ 与第三个约束里的 $a$ 的值相等？上一小节我们已经介绍过，在 groth16 里是依靠 trusted setup 的；但在 plonk 里不能这么干，所以我们要优化这个约束，把它变成两组约束：

可以看到两个大括号把等式分成了两组，上面一组约束是我们运算逻辑的约束，不同约束之间的变量是没有关系的，我们称之为门约束 （gate constrains）；下面一组约束是变量之间的约束，它们约束了不同变量之间的取值，哪些必须相同，我们称之为 copy constrains（copy constrains 来自 plonk 论文中的名字，是正经的术语； gate constrains 则只是大家有时候这么说，相对来说「不那么正经」）。

上面一组约束这里为什么习惯被叫成门约束呢？因为 plonk 约束里只有乘法和加法，并且参与运算的只能是变量（如 $a{\times}b=c$），不能像 groth16 那样可以有其它加减运算 （如 $(a-b){\times}c=d$），这就很像计算机芯片中的逻辑运算门，所以习惯被叫做门约束。

在 plonk 中， prover 和 verifier 要干的，不仅是要证明和验证上面一组约束的成立，也要证明和验证下面一组约束的成立。下面我们就分别介绍一下这两种约束。

2.1 门约束

在 groth16 中，我们把业务逻辑转变成 $(a + b) \times (c+d) = m+n$ 这种形式的多个等式，组成约束等式，比如：

由于有 3 个约束等式，所以我们选择三个点（比如 $1, 2, 3$）定义多项式 $l(x)$ 、$r(x)$ 和 $o(x)$ 。比如令 $l_a(x)$ 经过点 $(1,2,3)$ 时的取值为 $(1,0,0)$；令 $l_w(x)$ 经过点 $(1,2,3)$ 时的取值为 $(0,1,0)$；令$r_b(x)$ 经过 $(1,2,3)$ 时的取值为 $(1,-1,0)$ ；…… 。我们就可以得到每个变量对应的多项式 $l_a(x)$, $l_b(x)$ …, $r_a(x)$ , $r_b(x)$, …, $o_a(x)$, $o_b(x)$, …. 。然后当 witness 产生时，我们可以用 witness 的值和这些变量多项式组成 $L(x)$ 、$R(x)$ 和 $O(x)$ 。

但在 plonk 中，我们不把业务逻辑转变成上述形式，而是使用下面的等式进行转换：

这里面 $a$, $b$, $c$ 是变量，$q_L(x)$ 、$q_R(x)$ 、$q_O(x)$ 、$q_M(x)$ 和 $q_C(x)$ 是多项式，下标中的大写字符分别代表 Left 、Right 、Output 、Multiply 、Constant。

上面的这个等式，可以用来表示加法、乘法、常量相等三种运算的。比如我要表示 $a \times b = c$ ，那么可以令：

就可以得到 $0 \cdot a + 0 \cdot b + (-1) \cdot c + 1 \cdot (a\times b) + 0 = 0$ ，即 $a \times b = c$ 。 如果我要表示 $a+b=c$ ，可以令：

如果我要表示 $a = 10$ ，可以令：

可以看到，用这个等式的规则进行转换，也可以表示前面我们提到的门约束。为了读起来方便，我们把前面的门约束在这里再写一遍：

使用上面的等式的规则进行转换，可以得到：

到这里你可能会产生直觉：应该可以插值产生多项式吧？没错，到这一步，我们可以通过插项来定义多项式 $q_L(x)$、$q_R(x)$ 、$q_O(x)$ 、$q_M(x)$ 、$q_C(x)$ 了。比如上面有 8 行，我们可以随便选 8 个点，比如 $(1,2,3,4,5,6,7,8)$ ，令 $q_L(x)$ 在这 8 个点的值分别是 $-1,0,0,1,1,1,1,0$ ；其它的 $q_R$ 、$q_O$ 等也类似。

有了 $q_L(x)$ 、$q_R(x)$ 等多项式，我们可以组成一个新的多项式：

注意这里我们不再需要后面的 $=0$ 了，因为现在已经变成了多项式，不再是等式了。

不过目前这个多项式里的 $a$ 、$b$ 、$c$ 仍然是一个变量值，我们还无法用这个多项式代表整个的门约束。解决方法也很简单，把 $a$ 、$b$ 、$c$ 也插值成多项式就行了（比如让 $a(x)$ 在 $(1,2,3,4,5,6,7,8)$ 这 8 个点的取值分别是 $(a_1,0,a_2,m_{32},m_{42},y,m_{62},w)$），所以我们得到了：

读者请注意，我们前面有点颠倒了因果关系。正常情况下，是因为有了 $q_La+q_Rb+q_Oc+q_M(a \times b)+q_C=0$ 这套转换规则，才能把具体业务逻辑转换成门约束；但我们前面介绍的时候，先提了一下约束里只能是两个值相乘或相加，就直接把门约束等式写了出来，然后才介绍了转换规则。这样做是为了方便介绍，但需要知道，是先有了转换规则，才能生成这样的门约束等式（正是因为这样的转换规则，才能解释为什么约束里只能是两个值相加或相乘，而不能像 groth16 那样可以是两个加减运算相乘）

2.2 copy constrains

刚才我们介绍了门约束，以及如何在 plonk 中把门约束转变成多项式。但在门约束中，我们并没有规定不同约束间的变量必须相等，即使它们可能是同一变量。如果不加其它限制，我们完全可以赋给他们不同的值，然后所有的门约束等式依然可以成立。所以我们必须限制不同约束等式之间同一变量的取值，就像我们在 groth16 中做的那样。在 plonk 中这叫做 copy constrains 。

但是如果不像 groth16 那样，在 setup 阶段就对变量值作出约束，那只能在生成证明阶段约束了。也就是说，在 copy constrains 里，变量之间的相等性，也要通过约束放在证明过程中，这也是叫做 constrains 的原因。

为了好理解，我们先使用一个实例来介绍 copy constrains, 然后将实例泛化到一般情况。这里我们使用 plonk by hand 中的例子，即约束毕达哥拉斯定理等式：$a^2 + b^2 = c^2$ 。

首先我们将其写成约束等式的形式：

上半部分是门约束，我们刚才已经讨论过了，重点看下面的相等约束。在下面这组约束里是没有运算的，所以我们没法像门约束那样做去生成多项式；即使勉强认为有个加法（比如把 $a_1 = b_1$ 变成 $a_1 + (-b_1) = 0$ ） ，那又变成门约束了，而我们已经讨论过，门约束之间的变量是没有关系的，所以把这些相等约束变成门约束，那变量间的关系就又丢了。所以使用原来的老方法来把相等约束变成多项式是行不通的，我们得另相办法。

我们的目标是得到一个多项式，这个多项式在每个插值点，都可以约束某些变量的相等性（即生成多项式或 prove key 时，我们是按照某两个变量相等生成的，如果实际拿到 witness 后不相等，那得不到相同的多项式），直到最后一个插值点，可以约束所有变量的相等性。

copy constrains 在 plonk 中是如何做的呢？首先我们把这些变量排排行，并像往常一样，给它们对应一些插值点：

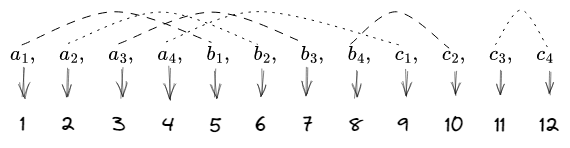
上图中还将相等的变量进行了连线。这里一共是 12 个变量，所以我们可以选择了 12 个值用于插什计算。但与之前不同的是，我们并不是要通过 $(1,a_1)$, $(2, a_2)$ 这些点来插值出来一个多项式。我们要插值出来三个置换多项式，分别记为 $S_{\sigma_1}$ , $S_{\sigma_2}$ , $S_{\sigma_3}$。所谓置换多项式，举个例子就很清楚了，比如 $a_4 = c_1$ ，$a_4$ 对应的插值点是 4, $c_1$ 对应的插值点是 9 ，所以 $S_{\sigma_1}(4) = 9$ 。

所以我们可以得到：

• $S_{\sigma_1}(x)$ 经过以下四个点： $(1,5)$, $(2, 6)$, $(3, 7)$, $(4, 9)$
• $S_{\sigma2}(x)$ 经过以下四个点：$(5,1)$, $(6,2)$, $(7, 3)$, $(8, 10)$
• $S_{\sigma_3}(x)$ 经过以下四个点：$(9, 4)$, $(10, 8)$, $(11, 12)$, $(12, 11)$

有了这三个转换多项式后，当我们随机选择两个值 $\beta$ 和 $\gamma$ 后，如果 $a_1$ 和 $b_1$ 相等，那么 $a_1+\beta \cdot 1 + \gamma$ 肯定等于 $b_1 + \beta \cdot S_{\sigma_2}(5) + \gamma$ 。所以我们可以这样来定义一组值：

其中 $n$ 门约束的数量，在上面的例子里，就是 4 。注意 $acc_i$ 并不是一个多项式，它们是一个具体的值。从上面的定义我们可以看到， $i$ 每加 1 ，如果 $a_i$ 、$b_i$ 或 $c_i$ 跟其它值相等，它们的就会被从分子和分母中约掉。

从 $acc_i$ 的定义中我们也可以看到，当我们根据变量之间的相等关系定义好 $S_{\sigma_1}$ 、$S_{\sigma_2}$ 和 $S_{\sigma_3}$ 后，等真正有了具体的变量值 $a_i$ 、$b_i$ 和 $c_i$ 后，这些变量之间的相等性是不是和定义 $S_{\sigma_1}$ 、$S_{\sigma_2}$ 和 $S_{\sigma_3}$ 时相同，会明确影响 $acc_i$ 的值。

3. 单位根

在介绍具体的 plonk 算法之前，我们还要先介绍一下单位根。我们前面的介绍中，当要插值得到一个多项式时，都是让多项式经过 $(0, 1, 2, …)$ 这样的点。但不其实不是必须的，任何点都可以，所以在 plonk 中，这些点都会使用单位根代替。所谓单位根，是指在一个有限域内，$x^n=1$ 的解。

比如，在 $\mathbb{F}_{17}$ 这个有限域内，所有的点是 0 到 16 。当 $n=4$ 时，$x^4=1$ 的根有 4 个，分别是：

单位根在 plonk 中使用 $\omega^i$ 来标记。就上面的例子来说，$\omega^0 = 1$, $\omega^1 = 4$, $\omega^2 = 16$ , $\omega^3 = 13$ .

有了单位根以后，上面我们所有例子中使用 $0, 1, 2, …$ 插值的，都可以使用 $\omega^0, \omega^1, \omega^2, …$ ；后面再遇到类似需要插值的时候，也是如此。

另外在前面介绍 copy constrains 的时候，当我们把所有变量排排行以后，需要 $3n$ 个点来进行插值（$n$ 为门约束的数量）。但我们刚才介绍了，单位根是 $n$ 个满足 $x^n=1$ 的值，那么在 copy constrains 中要计算 $x^{3n}=1$ 的值吗？不是的，在 plonk 论文里的方法是选择两个值 $k_1$ 和 $k_2$ ，用这两个值分别乘上 $\omega_0$ , $\omega_1$, …$\omega_{n-1}$ ，但到另外两个集合 ${k_1\omega_0, k_1\omega_1, …, k_1\omega_{n-1}}$ 和 ${k_2\omega_0, k_2\omega_1, …, k_2\omega_{n_1}}$ 。但 $k_1$ 和 $k_2$ 的选择是有要求的，即乘以 $k_1$ 生成的集合中的元素不能与原单位根集合中的元素重复；乘以 $k_2$ 生成的集合中的元素不能与前面两个集合中的元素重复。

4. 最终证明过程

4.1 符号约定

在后面的描述中，我们使用 $n$ 代表门约束的数量； $w_i$ 代表所有 input ，其中 $i \in [3n]$ 。（$w$ 可以理解成 witness 的第一个字符）。在所有的 input 中，所有 public input 组成的集合记为 $\mathscr{l}$ （注意这与 groth16 中的定义不一样，groth16 是前 $\mathscr{l}$ 个，而这里是个集合）。

这里再强一下所有 input 的排列方式。由于门会用到 3 个值：2 个输入 1 个输出，所以有 $n$ 个门的时候，会有 $3n$ 个 input ；这 $3n$ 个 input 的索引方式（排排行的方式）是：所有门的左输入放在 0 到 $n-1$ 的位置；所有门的右输入放在 $n$ 到 $2n-1$ 的位置；所有门的输出放在 $2n$ 到 $3n-1$ 的位置。

其它在前面我们介绍的过程中已经出现过的符号， 这里就不再赘述了。

4.2 要证明什么

prover 要证明的其实主要有两件事情，一是门约束；二是 copy constrains 。

对于门约束，其实就是证明：

（注意上面 $w$ 变量下标的不同）

而对于 copy constrains ，其实就是要证明：

这里 $\sigma(i)$ 的意思是：如果第 $i$ 个变量与第 $j$ 个变量相等，那么 $\sigma(i) = j$

$w_i = w_{\sigma(i)}$ 这个等式很直接，但证明它并不那么直接……

4.3 证明过程

这里我们根据 plonk 论文里的内容，描述一下整个证明过程。其中会尽量根据自己的理解，加入一点说明。

另外论文里并没有明确指定交互式还是非交互式，所以有时候用到一些挑战值（challenge value）时，都是使用 $\mathcal{H}$ 来代表一个生成随机数的哈希函数，并且用 $\mathcal{H}$ 来生成这些挑战值。所以如果是交互式证明，这些挑战值可以是 verifier 发送给 prover 的；如果是非交互式，可以使用 Fiat-Shamir transformation 变成非交互式的证明（当然我理解也可以将这些挑战值放到 trusted setup 中）。

注意 $\mathcal{H}$ 与普通生成随机数的方式不同，verifier 也是可以计算出和 prover 相同的挑战值的（只有这样 verifier 才能完成验证），但特别的地方在于在 prover 计算出这个值之前，任何人包括 prover 自己都无法预将会得到一个什么值。

另过要提一下的是，在证明过程中会用到一个多项式 $Z_H(x)$ ，其实就是「商多项式」，也就是可以整除其它多项式的多项式。如果看过之前 groth16 的相关文章，应该对这个概念比较熟悉。不过由于我们使用的是单位根，所以 $Z_H(x)$ 可以不必是 $(x-\omega_1)(x-\omega_2)…(x-\omega_n)$ ，而是 $Z_H(x) = x^n - 1$ ，因为单位根本身就是 $x^n=1$ 的解。

4.3.1 提前准备

跟 groth16 一样，plonk 也需要有 trusted setup 的过程，只不过这是一个比较通用的、与电路无关的 setup （通用的意思是，一个人 A 发起了 trusted setup 生成了一些数据，如果你相信这个过程，你就可以直接拿来这些数据，用在自己项目中的 prover 里）。

我们已经知道，trusted setup 主要是为了随机加密的随机数，我们用 $s$ 来表示。在 plonk 中我们需要用到 $s$ 的最高 $n+5$ 次幂的值，所以我们需要从 trusted setup 中得到以下值：

在 plonk 论文中，这里的值用 $x$ 表示，但我觉得还是 $s$ 更贴切更好理解，所以这里就不跟论文里保持一致了。

除了 trusted setup 中的值以外，prover 自身还要准备好 witness 。我们前面提到过，witness 用 $w_i$ 表示，一共有 $3n$ 个，其中所有 public input 组成集合 $\mathscr{l}$ 。

prover 还要准备好一类数据，就是选择子们 $q_{Mi}, q_{Li}, q_{Ri}, q_{Oi}, q_{Ci}, i \in {1,..,n}$ ， 以及利用这些选择子和单位根插值出来来多项式 $q_M(x), q_L(x), q_R(x), q_O(x), q_C(x)$。

prover 最后要准备的是转换多项式： $S_{\sigma_1}(x), S_{\sigma_2}(x), S_{\sigma_3}(x)$ ，它们的意义在介绍 copy constrains 时已经介绍过了。

在 plonk 论文中有一个 $L_i(x)$ ，每个值与 $L_i(x)$ 相乘，就得到了多项式，比如 $q_M(x)$ 在论文中是这样得到的：

这里的 $L_i(x)$ ，是基于单位根的拉格朗日基本多项式，也叫做插值基函数。从名字就可以看出来，它是拉格朗日插值法里的一个基本函数，这时我们不对拉格朗日插值法做过多介绍，你只要知道，将相应的值与 $L_i(x)$ 相乘，就可以得到插值出来的多项式。比如 $n=3$ 时，$q_{M1}= 1, q_{M2}=0, q_{M3}=2$ ，那么可以如下方法得到 $q_M(x)$：

事实上这就是拉格朗日插值法，但这不是我们本篇文章的重点

所以在论文里如果你遇到类似乘以 $L_i(x)$ 地方，可以直接在脑子里换算成一个多项式就可以了。

下面我们就可以正式开始证明过程了。plonk 的证明过程分 5 步，每一步称为 Round ，我们下面一一介绍。

4.3.2 Round 1

这一步我们要根据所有 input ，计算出变量多项式（wire polynomials）$a(x)$, $b(x)$, $c(x)$ 。

首先 prover 要生成随机数 $b_1, …, b_9$ ，然后计算多项式：

注意 $Z_H(x) = x^n-1$。另外这里就用到了前面介绍的利用 $L_i(x)$ 生成多项式的方式。

在得到 $a(x)$ 、$b(x)$ 和 $c(x)$ 以后，prover 利用 trusted setup 中的值，计算得到：

$[a(s)]_1$ 就是表示 $g_1^{a(s)}$ ，相信如果看过之前 groth16 系列的文章，这里的计算和表示方式应该不难理解。

4.3.3 Round 2

在 round 2 这一步，prover 的任务是计算 permutation polynomial 。

首先要得到 permutation challenges value $\beta$ 和 $\gamma$ ，论文里是使用 $\mathcal{H}$ 生成的，我们在前面也提过，它的意义就是生成前谁也无法预测将会生成什么值；但生成后其他人（比如 verifier）也可以生成相同的值。

然后代表 permutation polynomial 的 $z(x)$ 定义如下：

其中 $acc(x)$ 是我改上去的，根据论文原文， $acc(x)$ 等价于：

注意上面 $w_j$ 等带下标的字符是小写字母 w ，代表的是 witness ；$\omega^j$ 等带指数的字符是希腊字母 omega ，代表的是单位根。

可以看到如果使用 $acc(x)$ 代表后面这一堆，$z(x)$ 其实非常简单。所以这里我们重点看一下 $acc(x)$ 。

$acc(x)$ 里使用了大量的 $L_i(x)$ ，我们把它简化一下，把 $\prod$ 部分先用 \({acc_i},{i \in \{1,..,n\}}\) 代替，并令 $acc_0=1$ ，则：

前面我们提到过，论文里出现 $L_i(x)$ 实际是就是在使用插值计算多项式，所以这里多项式 $acc(x)$ 实际上就是经过 $(\omega^0, acc_0)$ , $(\omega^1, acc_1)$, $(\omega^2, acc_2)$ , …, $(\omega^{n-1}, acc_{n-1})$ 这些点的多项式。

现在我们再来看 $acc_i$ 的值是怎么来的。$acc_0 = 1$ 是硬规定的，这个不说。那么对于 $i>=1$ 时：

这是一个累乘等式，结合 $acc_0 = 1$ 的规定，其实也可以写成：

我感觉这样看上去更好理解一些。

现在我们应该看一下上式中后面那个分式了，但在些之前，我们先回顾一下相关细节。 \(\sigma^*\) 是置换函数，我们前面提过，把变量排成一行，每个变量对应一个根；如果第 $i$ 个变量和第 $j$ 个变量相等，那么 $\sigma^*(i)$ 就等于第 $j$ 个变量对应的根。我们前面也提到过，我们真正只找需找到 $n$ 个单位根 $\omega^i,{i\in {0,..n-1}}$，然后找出 $k_1$ 和 $k_2$ 两个值，所以第 $n+i$ 个变量对应的根就是 $k_1\omega^i$ ，第 $2n+i$ 个变量对应的根就是 $k_2\omega^i$ 。

现在我们再来看这个分式。你会发现这个分式其实就是把 $w_i$ 的等式累乘给 $acc_i$ ，但有个特殊现象：每当新增加一项 $w_i$ 的分式时，如果 $w_i$ 或 $w_{n+i}$ 或 $w_{2n+i}$ 跟之前任何某个变量（假设为 $w_j$）相等，那么分子上对应的式子（ $w_i + \beta\omega^i+\gamma$ 或 $w_{n+i}+\beta k_1\omega^i+\gamma$ 或 $w_{2n+i}+\beta k_2\omega^i + \gamma$ ）就会与之前 $w_j$ 在分母上的式子（$w_j + \sigma^*(j)\beta+\gamma$ ）抵消掉；同样如果之前某个变量与新增的 $w_i$ 或 $w_{n+i}$ 或 $w_{2n+i}$ 相等，之前分子上的式子也会与新增的分母上的式子抵消掉。所以我们可以得出结论，每个 $acc_i$ 的值都是由不相等的变量决定的，相等的变量会抵消掉。

然后，我们再进一层。置换函数 \(\sigma^*\) 是在生成 proof 之前就定义好了，更准确的说，是在有 witness 之前就定义好了，并且并不保密，人尽皆知，verifier 也会知道。所以有了 witness 后，如果原来 \(\sigma^*\) 规定好的两个变量应该是相等的，但在 witness 中不相等，就肯定会被 verifier 检查出来。所以通过这种方式，保证了变量之前的相等关系。

有了 $z(x)$ 以后，prover 利用 trusted setup 中的值，计算得到：

4.3.4 Round 3

这一步 prover 的任务是计算商多项式（quotient polynomial）$t(x)$ 。

首先要生成 quotient challenge value $\alpha = \mathcal{H}(transcript)$ 。

然后计算 $t(x)$ ：

可以看到之所以叫商多项式，是这里除了 $Z_H(x)$ 。

$PI(x)$ 是 public input 多项式，顾名思义就是 public input 插值出来的多项式，它的定义如下：

这个多项是 verifier 也是知道的，因为它的 public input 插值出来的嘛

不过上面我们得到的 $t(x)$ 的阶数很高，达到了最高 $3n$ 次方，所以 plonk 论文中对它进行了折分，折成了 3 个最高 $n$ 次方的多项式。拆分方法也很简单，就是阶数较低的项组成一个多项式 \(t'_{lo}(x)\) ；中等阶数的项抽出 $x^n$ 后，组成 \(t'_{mid}(x)\) ；阶数比较高的项抽出 $x^{2n}$ 后，组成 \(t'_{hi}(x)\) 。所以：

然后选择随机数 $b_{10}$ 和 $b_{11}$ ，令：

现在，我们将 $t(x)$ 定义为：

你会发现这里的 $t(x)$ 的定义其实与刚才 \(t(x) = t'_{lo}(x)+x^nt'_{mid}(x) + x^{2n}t'_{hi}(x)\) 这个定义是一样的，但我们使用随机数 $b_{10}$ 和 $b_{11}$ 对其加入了随机性，保证了零知识性。

最终，prover 利用 trusted setup 中的值，计算得到：

4.3.5 Round 4

这一轮比较简单。首先生成 evaluation challenge value $\mathfrak{z}$ ：$\mathfrak{z} = \mathcal{H}(transcript)$ 。 然后计算以下值（opening evaluations）：

其中这个 $\mathfrak{z}$ 值，就相当于批量多项式承诺中的 $z$ 值 。也就是说 plonk 要证明自己拥有的多项式在 $\mathfrak{z}$ 这个点的取值（另一个点是 $\mathfrak{z}\omega$，我们后面会提到）。

4.3.6 Round 5

这一轮用来计算两个大的多项式 $W_{\mathfrak{z}}(x)$ 和 $W_{\mathfrak{z}\omega}(x)$ ，这两个多项式融合了前面我们得到的所有多项式。然后我们输出这两个多项式的多项式承诺。

但在计算 $W_{\mathfrak{z}}(x)$ 和 $W_{\mathfrak{z}\omega}(x)$ 之前，我们要先计算线性多项式（linearisation polynomial） $r(x)$：

可以看到 $r(x)$ 与 $t(x)$ 很像，只不过很多很多多项式都被 round 4 中计算出值替换了。这是因为这里构造的 $r(x)$ 是有根 $\mathfrak{z}$ 的，即 $r(\mathfrak{z}) = 0$ 。我们来看看是如何做到的。

首先看 $r(x)$ 定义的最后一行 $t_{lo}(x)+\mathfrak{z}^nt_{mid}(x)+\mathfrak{z}^{2n}t_{hi}(x)$ 的部分。这部分和 $t(x)$ 的定义 $t_{lo}(x) + x^nt_{mid}(x)+x^{2n}t_{hi}(x)$ 很像。更重要的时，当 $x=\mathfrak{z}$ 时，这部分就是 $t(\mathfrak{z})$ 。

不过还记得前面原始的 $t(x)$ 定义吗？它被整个的除以了 $Z_H(x)$ （所以被称为商多项式）。$r(x)$ 定义的最后一行正好给乘了个 $Z_H(\mathfrak{z})$ ，所以当 $x=\mathfrak{z}$ 时，上面 $r(x)$ 定义的最后一行可以折分成：

在 round 4 我们计算出来 $\overline{a}=a(\mathfrak{z})$, $\overline{b}=b(\mathfrak{z})$, $\overline{c}=c(\mathfrak{z})$, \(\overline{s}_{\sigma1}=S_{\sigma1}(\mathfrak{z})\), \(\overline{s}_{\sigma2}=S_{\sigma2}(\mathfrak{z})\), $\overline{z}_{\omega} = z(\mathfrak{z}\omega)$ . 所以上面这个折分后的 $r(\mathfrak{z})$ 的最后一行，与 $r(\mathfrak{z})$ 定义中除最后一行的前面部分，完全相等。所以最终，$r(\mathfrak{z}) = 0$ ，即 $r(x)$ 有根 $\mathfrak{z}$ 。

然后 prover 还需要生成一个 opening challenge $v = \mathcal{H}(transcript)$ 。

有了 $r(x)$ 和 $v$ ，我们就可以定义 $W_{\mathfrak{z}}(x)$ ：

我们刚才已经分析过，$r(x)$ 有根 $\mathfrak{z}$ ；而在 round 4 中我们计算得到 $a(\mathfrak{z}) = \overline{a}$ , $b(\mathfrak{z}) = \overline{b}$, $c(\mathfrak{z}) = \overline{c}$, \(S_{\sigma1}(\mathfrak{z}) = \overline{s}_{\sigma1}\), \(S_{\sigma2}(\mathfrak{z}) = \overline{s}_{\sigma2}\), 所以 $W_{\mathfrak{z}}(x)$ 中分子中的每一项都有根 $\mathfrak{z}$ ，所以它们是可以被 $x-\mathfrak{z}$ 整除的。

接下来需要定义 $W_{\mathfrak{z}\omega}(x)$ ：

在 round 4 中我们计算得到 \(z(\mathfrak{z}\omega)=\overline{z}_{\omega}\) ，所以分子部分 $z(x)-\overline{z}_{\omega}$ 有根 $\mathfrak{z}\omega$ ，是可以被 $x-\mathfrak{z}\omega$ 整除的。

有了 $W_{\mathfrak{z}}(x)$ 和 $W_{\mathfrak{z}\omega}(x)$ 后，prover 就可以利用 trusted setup 中的值计算得到：

注意，还记得我们前面介绍批量多项式承诺的文章里，最终的验证等式里有 $W$ 和 $W’$ 吗？正是这里的 $W_{\mathfrak{z}}(x)$ 和 $W_{\mathfrak{z}\omega}(x)$ 。所在 plonk 算法中，prover 其实是要向 verifier 证明，$W_{\mathfrak{z}}(x)$ 和 $W_{\mathfrak{z}\omega}(x)$ 两个多项式分别经过点 $\mathfrak{z}$ 和 $\mathfrak{z}\omega$ 。

最终，prover 输出证明：

4.4 验证过程

现在我们来聊一下 verifier 的验证过程。首先我们要明确，以下数据是 verifier 和 prover 是都知道的：

从这里也可以看出，$q_M(x)$, $q_L(x)$, $q_R(x)$, $q_O(x)$, $q_C(x)$, $S_{\sigma1}(x)$, $S_{\sigma2}(x)$, $S_{\sigma3}(x)$ 这些多项式是公开的，verifier 也知道。其实也好理解，因为这些多项式只定义了 witness 变量之间的关系，并没有涉及到具体的变量值；并且虽然定义了 witness 变量之间的关系，但 verifier 也几乎不可能用这些多项式复原出这些关系，所以这些多项式是完全可以公开的，也是必须公开的。因为 verifier 使用这些多项式去验证提交的 proof 时，如果 prover 擅自改了这些多项式， verifier 就肯定会验证失败。

接下来，verifier 可以接收 prover 发送过来的 proof ，即 $\pi_{SNARK}$ ；以及所有 public input $w_i,{i \in [\mathscr{l}]}$ 。

然后 verifier 计算所有挑战值 $\beta$, $\gamma$ , $\alpha$, $\mathfrak{z}$, $v$, $u$ 。之前我们提到过，prover 使用 $\mathcal{H}$ 计算出来的挑战值，verifer 也是可以计算出来的。

有了以上准备后，首先用值 $\mathfrak{z}$ 计算以下多项式的值：

然后为了节省 verifier 的计算量，我们把 $r(x)$ 中的常量部分拿出来，先计算好：

然后让 $r’(x) = r(x) - r_0$，得到 $r(x)$ 中非常量部分的多项式。

接下来我们计算批量多项式承诺（batched polynomial commitment）的第一部分 $[D]_1 = [r’]_1 + u \cdot [z]_1$ ：

这里 $[D]_1$ 的等式是代入 $[r’]_1$ 后整理的最终结果，省略了中间计算过程，因为 $r(x)$ 是一个很长的多项式，中间计算过程比较繁锁，这里就不详细展开了。

然后计算整个的批量多项式承诺 $[F]_1$ ：

再然后计算 group-encoded batch evaluation $[E]_1$ ：

最终，verifier 使用双线性映射，验证以下等式是否成立，成立则证明 proof 是正确的：

4.5 验证的意义

这一通算下来，你可能会有疑问：为什么要这么算呢？这是在干吗？这时候我们就需要再提一下之前文章 里介绍的批量多项式承诺了。在那篇文章的最后，我们得出批量多项式承诺的验证等式为：

注意这里把等号左右两边调换了一下，方便与 plonk 的验证等式对比

之前在 round 5 中我们也介绍过，$W_{\mathfrak{z}}$ 就是等式 $(b)$ 中的 $W$ ，$W_{\mathfrak{z}\omega}$ 就是 $W’$ 。而 $(b)$ 中的随机数 $r’$ 在 plonk 的验证等式中，在等式 $(a)$ 则使用 $u$ 代表。即：

所以：

可以看到，等式 $(a)$ 和 $(b)$ 的等号左侧是完全等价的，一个意思。

我们再来看看等号右边。round 5 中我们也提过，plonk 最终要证明 $W_{\mathfrak{z}}(x)$ 在点 $\mathfrak{z}$ 的值和 $W_{\mathfrak{z}\omega}(x)$ 在点 $\mathfrak{z}\omega$ 的值，所以等式 $(b)$ 中的 $z$ 就是等式 $(a)$ 中的 $\mathfrak{z}$ ，且 $(b)$ 中的 $z’$ 就是 $(a)$ 中的 $\mathfrak{z}\omega$ 。即：

所以：

可以看到只要 $(a)$ 中的 $[F]_1 - [E]_1$ 等价于 $(b)$ 中的 $F$ ，$(a)$ 和 $(b)$ 也是等价的。那这俩是否等价呢？

在 $(b)$ 中 $F$ 代表什么意思呢？我们把介绍批量多项式文章中对 $F$ 的定义拷贝过来：

可以看到，$F$ 由两部分组成，我们一个一个看。

我们先看第一部分 \(\sum\limits_{i=1}^{t_1}cm_i - \sum\limits_{i=1}^{t_1}[f_i(z)]_1\) 。由于 $cm_i$ 是计算商多项式 $W$ 的多项式的承诺，对应在 plonk 算法中就是计算商多项式 $W_{\mathfrak{z}}(x)$ 的多项式的承诺， 也就是 round 5 中计算 $W_{\mathfrak{z}}(x)$ 时的分母去掉减法后面的部分（$r(x)$ 后面没有减去什么东西，因为 $r(x)$ 本身就有根 $\mathfrak{z}$，这个我们在 round 5 中说过了）。所以 $\sum\limits_{i=1}^{t_1}cm_i$ 价于 ：

而 $\sum\limits_{i=1}^{t_1}[f_i(z)]_1$ 则等价于上面各多项式在 $\mathfrak{z}$ 点的取值，即：

这里面大多数值，我们在 round 4 中已经计算好了，并且给了新的符号；而在 round 5 中我们也说明过，$r(x)$ 有根 $\mathfrak{z}$ ，即 $r(\mathfrak{z}) = 0$ ，所以上面等式应该是：

我们再来看看第二部分 \(\sum\limits_{i=1}^{t_2}cm'_i - \sum\limits_{i=1}^{t_2}[f'_i(z')]_1\) 。这里 \(cm'_i\) 是计算商多项式 $W’$ 的多项式的承诺，对应在 plonk 算法中就是计算商多项式 $W_{\mathfrak{z}\omega}(x)$ 的多项式的承诺。根据 round 5 中对 $W_{\mathfrak{z}\omega}(x)$ 的定义，\(\sum\limits_{i=1}^{t_2}cm'_i\) 应该等价于 $[z]_1$ 。而 \(\sum\limits_{i=1}^{t_2}[f'_i(z')]_1\) 则等价于 $z(x)$ 在 $\mathfrak{z}\omega$ 点的取值，这在 round 4 中已经计算好了，就是 \(\overline{z}_{\omega}\) 。

所以到目前为止，我们得到上面等式 $(b)$ 中的 $F$ 等价于：

整理一下，把减去的部分凑一起，得到：

我们再像 plonk 论文里那样，把 $r(x)$ 里常数部分拿出来，用 $r_0$ 表示，即 $r(x)=r’(x)+r_0$ 。所以上面等式 $[r]_1$ 就可以拆成 $[r’]_1+[r_0]_1$ 。然后把 $[r_0]_1$ 拿到减号后面，就变成了：

而在 plonk 最后 verifier 的验证中，$[D]_1$ 正好等式 $[r’]_1+u[z]_1$ ，所以上面等式也可以写成：

现在我们可以看到，上面式子中，减号前面的部分正好等式 verifer 验证等式中 $[F]_1$ 的定义；而减号后面的部分正好等式 $[E]_1$ 的定义。所以我们可以得出结论，前面验证等式 $(a)$ 中的 $[F]_1 - [E]_1$ 意义上和等式 $(b)$ 中的 $F$ 是完全一样的。可见 plonk 算法的整个过程，正是严格遵循批量多项式承诺算法的过程。

5. 总结

plonk 算法是目前零知识证明算法里应用最广泛的算法了，但由于引入了 copy constrains ，相比于 groth16 来说增加了很大的复杂性。不过万变不离其宗，从上面的分析我们也可以看到，整个 plonk 算法都是围绕批量多项式承诺展开的，只要理解了批量多项式承诺，就可以很好的理解 plonk 算法里大部分内容了。