本篇文章分析的源码地址为:https://github.com/ethereum/go-ethereum
分支:master
commit id: 257bfff316e4efb8952fbeb67c91f86af579cb0a
引言
目前以太坊中有两个共识算法的实现:clique和ethash。其中clique中PoA共识的实现,我们已经在之前的文章中介绍过;ethash是PoW共识的实现,也是本篇文章的主题。
ethash是目前以太坊主网(Homestead版本)的共识算法,除了必须的PoW的功能,ethash还考虑到了挖矿公平性的问题。因为内容较多,我们将介绍ethash的文章分成了两篇。本篇主要介绍ethash实现的相关理论和设计思想;下篇文章我们再通过具体的源代码,对这些设计思想进行验证。
什么是PoW
PoW的全称为Proof of Work,中文译为“工作量证明”。我们先看看维基百科上对PoW的解释:
工作量证明(Proof-of-Work,PoW)是一种对应服务与资源滥用、或是阻断服务攻击的经济对策。一般是要求用户进行一些耗时适当的复杂运算,并且答案能被服务方快速验算,以此耗用的时间、设备与能源做为担保成本,以确保服务与资源是被真正的需求所使用。此一概念最早由Cynthia Dwork和Moni Naor于1993年的学术论文提出[1],而工作量证明一词则是在1999年由Markus Jakobsson与Ari Juels.[2]所发表。现时此一技术成为了加密货币的主流共识机制之一,如比特币所采用的技术。
从维基百科的上来看,PoW是一种经济对策,而目前应用最火的就是区块链项目。因此将这个解释应用于区块链的语境中,我们可以得到PoW的两个特点:一是方便向其它结点证明自己确实做了很多计算工作、有资格拿到某些权力;二是其它节点非常容易验证这一事实。
为什么区块链要有PoW呢?我们知道所有区块链项目每隔一定时间都要求出一个区块,同时我们也知道区块链项目是分布式的、去中心化的,没有中心节点指挥着其它节点“有序”的出块。既然没人指挥,就需要在每次出块时有一种所有节点都认可的确权机制:出块的人必须满足某个要求,并且其它节点可以验证这个满足条件。这种确权机制被称之为共识。
PoW也是一种共识。在之前介绍clique的文章里,我们介绍了一个共识:PoA,它是通过“选举专家”来确认出块权的。而与PoA不同的是,PoW是一个人人都可能有出块权的共识机制:在每次出块时,只要你的计算工作做得够快,抢在别人之前计算出满足条件,你就有权出块。我们不能说这些办法谁优谁劣,根据区块链项目的不同,每种共识都有它适用的情境。
所以我认为PoW的存在的主要意义,是可以使任何人参与区块链项目的出块。
但若想拿到出块权就要拼“计算能力”了,你的机器性能越好、计算得越快,就越能快速的得出满足条件并进行出块。而计算得慢的机器,还没等算出“满足的条件”,这人个块已经被别人出了,只能转而进行下一个块的出块计算,但仍会被性能好的机器抢先。如此循环,性能差的机器白白进行了无用的计算,却很难出一个块。
通过以上的描述,我们可以这样总结PoW:
PoW用来对人人可以参与的区块链项目的出块权进行确权。确权的方式是通过计算满足一定的条件。这个计算必须是复杂的、耗时的;而条件的验证最好是非常简单能快速完成的。
PoW的基础实现方案
现在我们可以尝试想一下,如果让我们自己实现一套PoW代码,该怎么做。
通过前面的讨论,我们可以总结出PoW需要具有以下条件:
- 有一个确定的验证方式
- 计算复杂:得到正确结果的过程比较复杂和耗时,不能轻易得到正确的答案
- 验证简单:其它人可以轻易验证别人的结果是否满足
其实很自然的我们会想到,哈希计算就非常符合:哈希基本是单向的,想要从一个确定的哈希得知它是由哪个数据集计算出来的几乎是不可能的,但计算某一数据集的哈希值非常简单。因此我们可以这样设计:要想得到出块权,必须找到某一哈希对应的数据集。此种设计下,验证方式是确定的:只要比较哈希值是否相等就可以了;满足计算复杂的要求,要计算某一确定哈希对应的数据集是非常困难的;也满足验证简单的要求:一旦有人给出一个数据集和其哈希值,我们可以很快验证其正确性。
相信读者看到这里肯定会立刻心生疑问:如果使用的是像md5甚至sha256这种哈希算法,从哈希值得到其对应的数据集几乎是不可能的,否则很多密码就该被破解了。这个设计,很有可能没有人能出得了块吧?
确实,现实中如果真这么设计,可能没有节点能给出正确答案(否则我们现有的加密世界真的就崩塌了)。既然严格的哈希值匹配几乎不可能,我们就换一个变通的方式,不严格匹配哈希值,而是匹配哈希值的特征。比如要求计算得到的哈希值必须至少含有一定数量的0字节;又比如我们将计算得到的哈希值看作一个整数,要求它必须小于某个特定的整数值。如此一来,要得到一个有效的哈希可就简单多了。
到目前为止,好像看上去万事大吉,所有PoW都已经满足了。确实,PoW没什么复杂的,上面的讨论基本上就可以作为一个PoW的实现框架了。但现实中的区块链项目通常还会考虑得更多一些,其中之一就是拉长时间维度来看待“计算复杂”这个问题。
我们知道计算机硬件是不断发展的,因此一些运算现在看来是“复杂的”,但在将来可能就变成了一个“简单”的计算。因此我们需要动态调整对计算结果的要求,让计算始终维持是“复杂的”,因而总是维持在一定的时间之内。比如我们把计算得到的哈希值作为一个数值时,小于1亿就是一个有效哈希;但当我们发现前一个块的出块时间距当前时间非常短时(也就意味着那个节点在很短时间就找到了有效哈希),我们把当前的有效哈希的最大值设置为1千万。因为要得到一个小于1千万的值比小于1亿的值难得多,这样就保证了这个计算始终是“复杂”的。
上面的讨论中我们一直没提及计算哈希的数据集从哪里来。其实可以使用的数据集很多,但应用得比较多的是区块的Header数据。如下所示:
type Header struct {
//其它字段
Nonce []uint8
}
一个区块的Header结构的其它字段都是有用的、不可随意改变的,因此想要不断调整Header的哈希,就得有一个可以随意调整值的字段,Nonce字段就是这个作用。通过不断改变Nonce的值,就可以不断改变Header结构的哈希,直到找到符合要求的哈希。
所以经过上面的讨论,我们可以使用以下方法实现一个基础的PoW:
- 使用哈希算法作为计算复杂、验证简单的保证
- 验证方式为将计算得到的哈希值作为一个数值,比较其是否小于某一阈值
- 根据前一个块的出块时间长短,阈值可以动态调整,以保证计算复杂度
- 哈希算法的数据源为新块的Header的哈希(保留Nonce字段可以随意更改)
ethash的实现方案
虽然以太坊是非常知名的区块链项目,但它的共识算法ethash的实现思路与我们刚才考虑的大体是一致的(你看,知名区块链项目的实现原理也不复杂嘛),只有哈希算法的数据源有较大的不同,这也是ethash与众不同之处。下面我们一一介绍ethash的关键实现。
ethash的设计逻辑可以在这篇文章中看到,由于分析的维度不一样,我并没有按照官方的文档进行介绍,而是按我的逻辑对一些方面进行重点分析,而另一些仅仅是提及了一下。
验证方式
在以太坊区块的Header结构体里,有一个Difficulty字段,它定义了当前块的“出块难度”。在验证时,要求计算得到哈希值作为一个整数必须小于Difficulty值。这与我们刚才讨论的方法完全一致。准确的话,ethash将计算得到的哈希值作为整数,与 $\frac{2^{256}}{\text{Header.Difficulty}}$ 这个值进行比较,小于这个值才是有效的哈希。
但基于ethash计算啥希的方法(后面我们会讨论),以太坊这里多进行了一步验证:在Header结构中还有一个MixDigest字段,ethash在计算哈希时会得到两个值,除了用来与Difficulty字段进行比较的哈希值,还有一个就是用来与MixDigest进行比较的哈希值。要想验证通过,这个啥希值必须与MixDigest字段中的一致。
因此ethash中验证方式可以总结为:
- 进行哈希计算得到两个啥希值:mix和result
- result作为一个整数值,必须小于 $\frac{2^{256}}{\text{Header.Difficulty}}$
- mix必须与header.MixDigest完全一样
此时你心中肯定急切想知道ethash到底是怎么计算哈希的吧?别着急,作为内容最多、最重要的一块,我们放到最后再说。下面我们先看一看如何动态调整Header.Difficulty字段。
动态调整Header.Difficulty
ethash实现了对出块难度要求的动态调整,以粗略保证出块的时间间隔的稳定。由于以太坊的版本升级和分叉,ethash中有多个动态调整的Header.Difficulty的方法,我们从最旧到最新一一分析一下。
Frontier版本
以太坊的发布分成了四个阶段:Frontier、homestead、Metropolis和Serenity,关于这些发布阶段的介绍,可以参考以太坊的博客文章和这个问答。这里我们只关注动态调整Header.Difficulty的原理。
在Frontier版本中通过以下公式对Header.Difficulty进行调整:
step = parent_diff // 2048
direction = 1 if block_timestamp - parent_timestamp < 13 else -1
expAdjust = 2**((block.number // 100000) - 2) if block.number >= 100000 else 0
Header.Difficulty = parent_diff + step * direction + expAdjust
这段公式是用python代码写的,因此我们对其中一些操作和变量作一个说明:
parent_diff: 父块的Header.Difficulty字段的值
block_timestamp: 新块的Header.Time字段的值
parent_timestamp: 父块的Header.Time字段的值
block.number: 新块的高度
//: 整数除法,比如3//2等于1,4//2等于2,5//2等于2。
**: 指数乘法,比如2**3等于8,2**4等于16。
x if condition else y: 这是python的语法糖,如果condition为true,这个表达式的值为x,否则为y。
这个公式表达了这样的含义:每个新块的难度值是根据父块的Difficulty值调整的;每次调整的基础大小为step(parent_diff // 2048),另加指数值expAdjust;如果父块的出块时间与当前块的时间相隔小于13秒,则增大一个step以稍微增加难度、延长当前块的出块时间,否则就减小一个step。
这个公式的动态调整体现在step * direction这一步的计算中:如果之前的出块时间太快,就增加一下难度出得慢一些;如果之前出块太慢,就减小一下难度出得快一些。但令人费解的是expAdjust,这是一个指数式,并且由块的高度作为变量。因此可以预见随着块的高度变大到一定程度,Difficulty将呈现指数级的增长,再也不是动态调整了。如下图红框部分的时间所示。
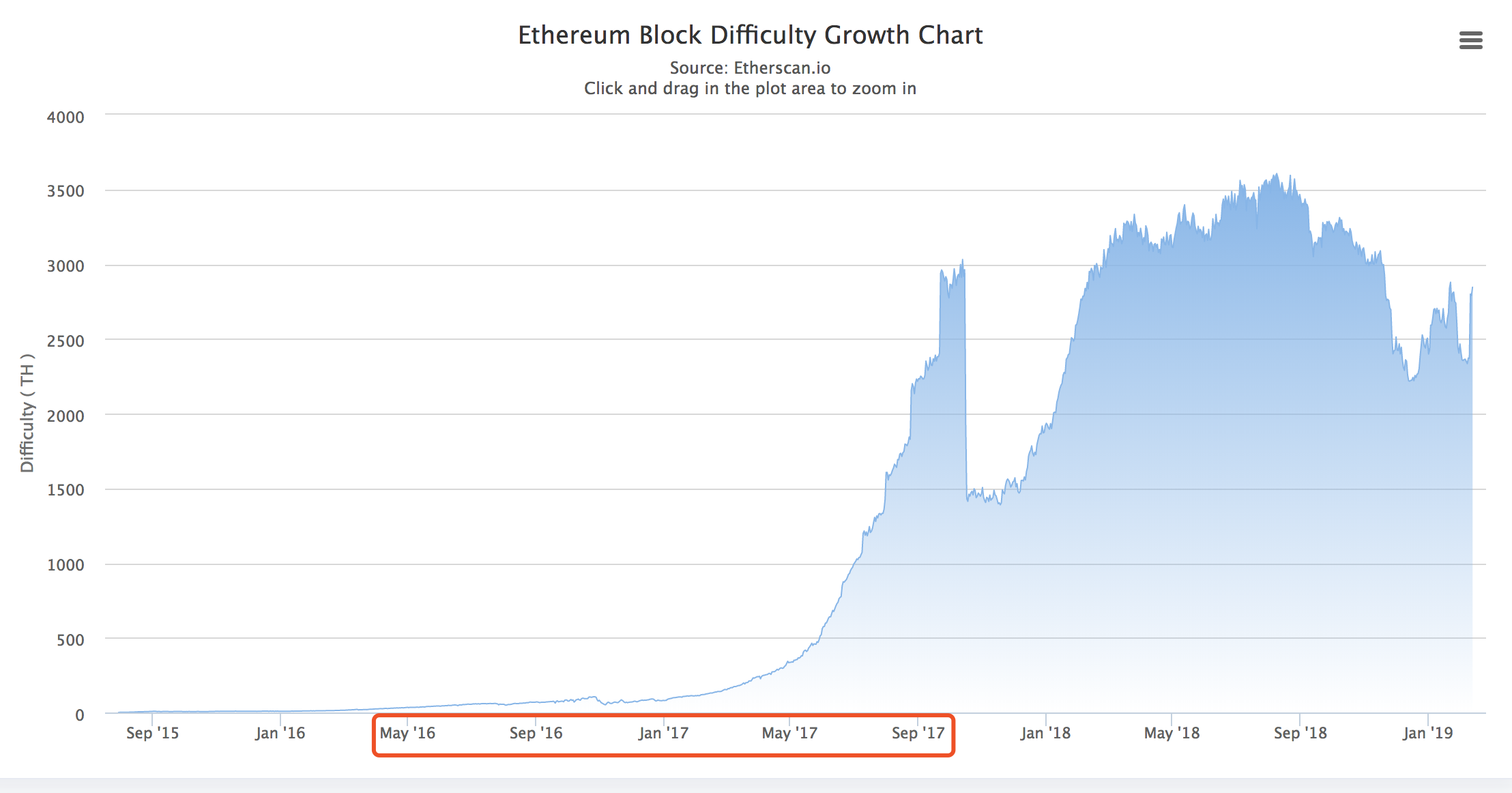
(关于为什么这张图中随后Difficulty值很快掉下来了,请看后面的分析)
你肯定会想为什么要这样设计。这样挖矿岂不是越来越难,很快就挖不了了?以太坊之所以这样设计,是因为以太坊一开始就计划着把PoW共识当作一个过渡,最终的以太坊将使用PoS(Proof of Stake,权益证明)作为共识,而弃用PoW。PoS是不需要挖矿的,因此在由PoW转向PoS的过程中如果处理不好,肯定会损害一些矿工的利益并引起他们的抵制(因为这些矿工可能投入了大量资金购买了矿机,但转向PoS后这些矿机就没什么用处了)。所以以太坊的设计者在动态调整的公式中加入了指数式这一部分,目的是希望大家有一个预期,从而平和的从PoW转向PoS(毕竟知道了是条死胡同,也就没人会一条道走到黑了)。以太坊的这个设计被称为“难度炸弹”,难度逐渐增加以至于很难或几乎不可能出块的阶段被称为“冰川时代”。
Homestead版本
在Homestead版本中,Header.Difficulty的计算公式又发生了变化,改成了这个样子:
step = parent_diff // 2048
direction = max(1 - (block_timestamp - parent_timestamp) // 10, -99)
expAdjust = 2**((block.number // 100000) - 2)
Header.Difficulty = parent_diff + step * direction + expAdjust
可以看到,与Frontier相比,唯一改变的就是direction的计算方法。在这个版本中不再将两个区块的时间间隔直接与13比较,而是取得其10的倍数。整个direction的计算达到了这样的效果:
- 如果出块时间间隔较小(block_timestamp - parent_timestamp < 10),则direction值为1。这将稍微增加新块的难度。
- 如果出块时间间隔在10秒至20秒之间,则direction值为0。因此除指数部分外,不会对难度进行改变。
- 如果出块时间间隔在20秒以上,则direction值为一个负整数,最小为-99。这将减小新块的难度,减小程度视时间间隔而定,间隔越长减小得越多。
与上一个版本相比,这主要有两个改动。一个是当两个块的时间间隔比较大时,难度值可以立即得到较大幅度的调整,这是由(block_timestamp - parent_timestamp) // 10决定的(之前版本中时间间隔再大,也只能调整一个step)。另一个是不再严格与13秒进行比较,而是以10为基础,进行粗略的调整。
这里有以太坊官方文档详细介绍了更改计算公式的原因。简单来说是他们发现有矿工总是出block_timestamp - parent_timestamp为1的块。因为这样会导致难度值一直在增加,少数人这样干还好,如果多数矿工都这么干,那么难度值会一直增加,这就失去了动态调整的意义。修改以后使用block_timestamp - parent_timestamp) // 10代替直接和13进行比较,可以阻止矿工设置时间间隔为1。(其实我没真正明白为什么这样就可以阻止,我认为只能鼓励大家不要设置时间间隔为1)。
另外文章中说这个计算方法可以粗略的控制出块时间平均值。可以证明使用新的公式,长期来看超过24秒的平平均出块时间是不可能的。这个地方我也没弄明白为什么,希望有读者知道能热心告知。
拜占庭(Byzantium)分叉
我们再来看看这么显示Difficulty变化的图:
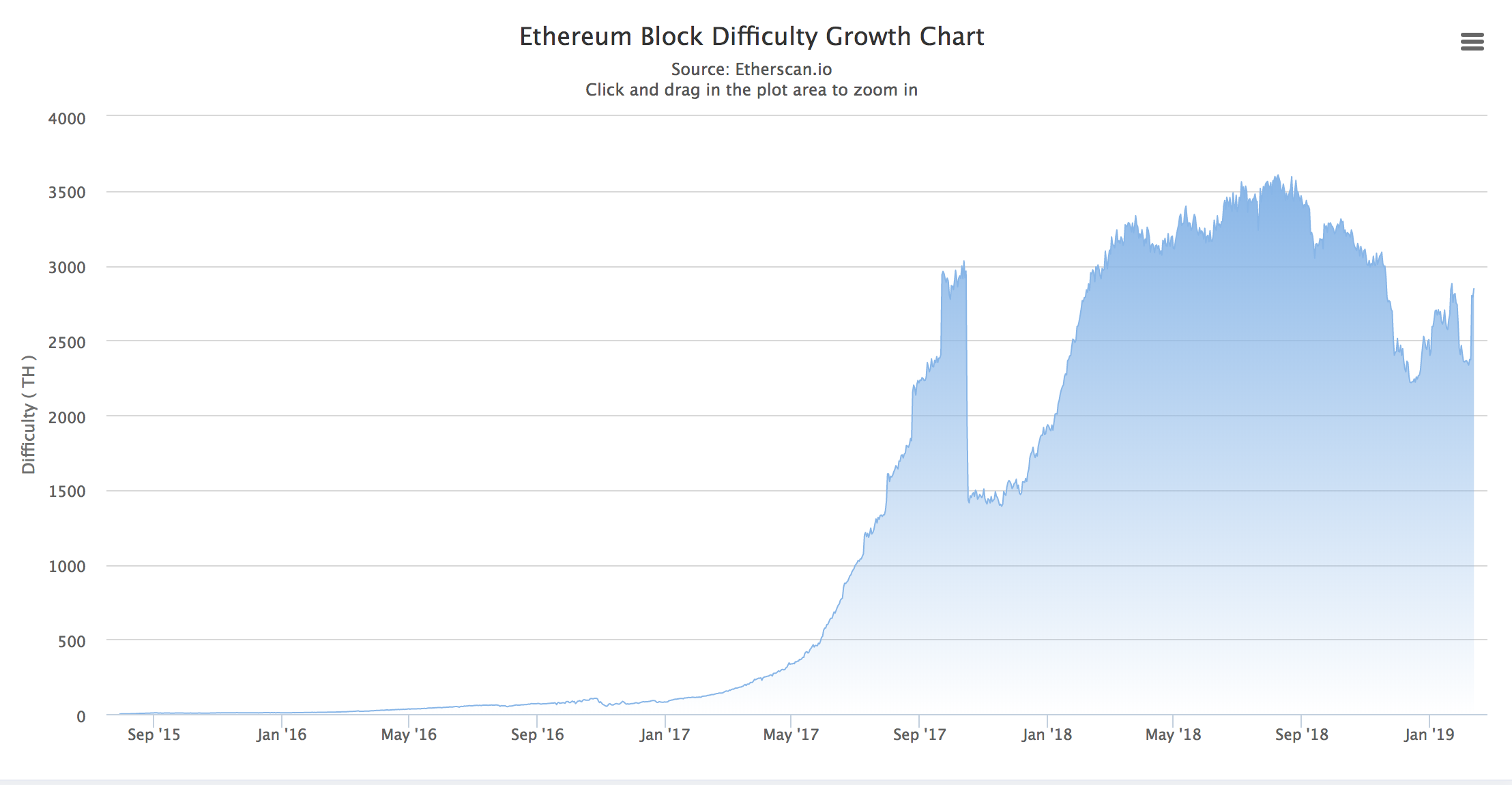
相信在前面这到这张图的时候,你就已经产生了疑问:为什么Difficulty值在2017年10月份的时候突然下降了好多呢?因为在这个时间点上以太坊进行了升级(分叉),更改了Header.Difficulty的计算方式。这一次分叉就是拜占庭分叉。新的计算方法如下:
step = parent_diff // 2048
direction = max((2 if len(parent.uncles) else 1) - ((timestamp - parent.timestamp) // 9), -99)
block_number = block.number if block.number < 2999999 else (block.number - 2999999)
expAdjust = 2**((block_number // 100000) - 2)
Header.Difficulty = parent_diff + step * direction + expAdjust
可以看到与Homestead版本比较有两个变化:一是direction的计算,二是指数部分的块高度的计算发生了变化。
direction部分的主要改动是增加了(2 if len(parent.uncles) else 1)这一计算。Homestead版本中这个值固定为1,这里改成了如果存在叔块则这个值为2。这达到的效果是如果存在叔块,则稍微增加一下出块难度、放缓一下出块节凑。
重点是指数部分的改动。由于“难度炸弹”已经发挥作用了,但转换到PoS的工作还没有就绪,所以以太坊作了一次分叉来延长“难度炸弹”发挥作用的时间。具体做法就是当块的高度超过3百万时(此时Homestead版本的“难度炸弹”已经很有威力了),将用于指数计算的高度减去3百万,从而使指数部分再次暂时变得可忽略。这一过程被称作“难度炸弹延迟”。
君士坦丁堡(Constantinople)分叉
Constantinople分叉是写此篇文章时最近的一次修改难度值的分叉。它与Byzantium分叉的计算方式完全一样,只不过又将“难度炸弹”的延迟高度提高到了5百万。看来转换到PoS的工作比以太坊团队预计的又延后了…….
此次修改的文档在这里。
哈希数据源
在前面我们讨论基础的PoW方案时,我们使用的是区块的Header作为计算哈希的数据源。但以太坊对PoW有更高的要求,希望ethash可以抵制ASIC矿机(Application Specific Integrated Circuit,专用集成电路,此处指专门设计用来挖矿的机器)。因此除了使用Header和Nonce字段,ethash还有更大一块数据集用来计算哈希。
你可能会想,为什么要抵制ASIC矿机呢?ASIC矿机是专门设计用来挖矿的机器,因此挖矿的能力肯定比普通机器高不少,有很多人为了能多挖矿而买非常多的这种矿机。这就有可能形成一种算力集中的现象:某一个或几个大的矿主手中的算力合在一起,可以超过总网一半以上的算力。虽然出于利益考虑这些矿主不太可能利用算力攻击这个区块链网络,但矿主却有项目布署的选择权,当开发社区想要对项目进行修改或升级时,如果矿主不同意,那么就无法完成新的布署。比特币就曾发生过矿主和开发者意见不统一而导致分叉的现象。
以太坊是如何抵制ASIC矿机的呢?简单来说,是通过内存限制来抵制的。原因有二,一是因为ASIC矿机中使用大内存比较昂贵;二是因为大量随机读取内存数据时计算速度就不仅仅受限于计算单元,更受限于内存的读出速度。
(但不得不说的是,2018年8月份比特大陆已经推出了以太坊的矿机,虽然具体效果未知,但仍算是突破了)
因此在ethash中,要计算哈希,需要先有一块数据集。这块数据集较大,初始大小大约有1G,每隔3万个区块就会更新一次,且每次更新都会比之前变大8M左右(与动态调整Difficulty类似,数据集的不断变大是为了应对硬件的不断发展)。计算哈希的数据源就是从这块数据集中来的;而决定使用数据集中的哪些数据进行哈希计算的,才是区块头部的数据和Nonce字段。
ethash中的这种方法可以称为”Dagger-Hashimoto”算法的变种。本文只专注于ethash的实现,因此不对原始的”Dagger-Hashimoto”算法进行说明,感兴趣的读者可以参看这里。
虽然以太坊对原来的”Dagger-Hashimoto”作了很大改动,但官方也没给一个新的名字,因此我们这里仍然使用这个名字,但分析的仍然是以太坊改动以后的版本。 我们会从总体的视角来看一下这个算法的概况和原理。
实际上”Dagger-Hashimoto”分两部分:Dagger部分和Hashimoto部分。Dagger算法用来生成数据集,Hashimoto使用数据集生成哈希。下面我们一一介绍。
为了描述方便,后面我们使用dataset来特指这个数据集。
Dagger
Dagger算法定义了dataset的生成方式和组织结构。那么dataset是如何组织的呢?
我们可以理解dataset为由多个item组成的巨大的数组,每个item是一个64字节的byte数组(其实可以理解成一条哈希,为了区分,我们称dataset的item为dataItem)。前面我们说过,dataset的初始大小约为1G,每隔3万个区块(一个epoch区间)就会更新一次,且每次更新都会比之前变大8M左右。
dataset虽然较大,但它的每个dataItem都是由一个缓存块(cache)生成的。缓存块同样可以看作是由多个item组成的数组,每个item也是一条哈希(为了区分,我们称cache的item为cacheItem)。缓存块占用的内存要比dataset小得多,它的初始大小约为16M。同dataset类似,每隔3万个区块就会更新一次,且每次更新都会比之前变大128K左右。
生成一条dataItem的计算过程是这样的:从缓存块中“随机”(这里的“随机”不是真的随机数,而是指事前不能确定,但每次计算得到的都是一样的值)选择一个cacheItem进行计算,得的结果参与下次计算,这个过程会循环256次。
缓存块是由seed生成的,而seed的值与块的高度有关。所以生成dataset的过程如下图所示:
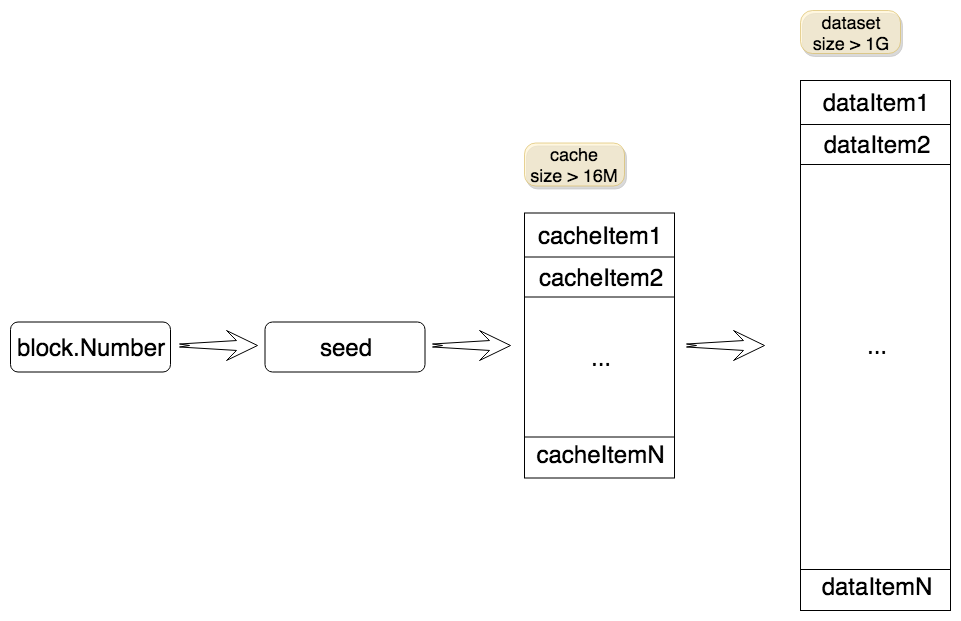
Dagger还有一个关键的地方,就是确定性。即同一个epoch内,每次计算出来的seed、缓存、dataset都是相同的。否则对于同一个区块,挖矿的人和验证的人使用不同的dataset,就没法进行验证了。
在以太坊中的文档中,称这个巨大的dataset为DAG。这篇文章里我们仍然统一称之为dataset。
可以看到,dataset的生成方式可以说是“分级”的:由一个简单的块的高度值,得到一个seed,进而生成缓存块;再由缓存块,生成1G多的dataset。这种“分级”的生成方式,在保证挖矿时必须占用大量内存时,使验证也比较简单。为什么呢?
一方面,在挖矿时,需要用到dataset中的数据(由挖矿算法决定的,参看后面对Hashimoto的介绍)。如果矿工不想占用这么大内存,就必须在挖矿时每次计算用到的dataItem。我们知道挖矿的过程是一个尝试的过程,且一般在尝试非常多次以后才能“挖出矿”;而每次尝试都会计算128个dataItem。这样无疑大大增加了挖矿的计算成本,逼迫矿工放弃这种做法。
另一方面,如果一个节点不想挖矿,只是收到区块后进行验证(如轻节点),那么这个节点可以不用保存并占用这么大一块内存,而是只保存比较小的缓存块就行了。在验证过程中如果缺少某个dataItem,使用Dagger算法可以通过缓存块计算得到这个dataItem。因为验证只进行一次,用不了多太多时间。
所以这里的关键点是挖矿需要多次尝试,而验证只需一次;单次的计算时间是可以接受的,但多次累加在一起对于挖矿来说就不可接受了。
这篇文章介绍了dataset存储方面的一些知识,感兴趣的读者可以参看,这里不再作介绍。
Hashimoto
下面我们再来说说Hashimoto部分,它的作用就是使用区块Header的哈希和Nonce字段、利用dataset数据,生成一个最终的哈希值。我们先看一下它的伪代码:
func hashimoto(headerHash, Nonce, datasetLookup) {
seed <- crypto.Keccak256([headerHash, Nonce])
seedHead <- uint32(seed[0:4])
mix <- [seed, seed]
for i := range 64 {
itemIndex <- generateIndexBy(mix, i, seedHead)
tmp <- [datasetLookup(itemIndex), datasetLookup(itemIndex + 1)]
mix <- aggregateWith(mix, tmp)
}
mix <- compressToAHash(mix)
return mix, crypto.Keccak256([seed, mix])
}
可以看到,hashimoto函数先用区块的Header哈希和Nonce值生成一个初始哈希,然后通过简单的计算(generateIndexBy)得到需要获取的dataset数据中的item索引。取到item以后,将其聚合到当前的mix变量中。
注意在这个函数返回后,ethash其实是验证第二个返回值是否符合要求,但以太坊会在区块的头部的MixDigest字段保存第一个返回值即mix值,在验证时需要这个mix的值与Header.MixDigest字段完全匹配。这一点在前面“验证方式”一节里也提到过了。
在以太网官文介绍ethash的这篇文章里,说上面伪代码中最后return语句中的crypto.Keccak256这一调用可以用来防DDos攻击,我是没想明白原因,如果有知道的读者还请告知。
总结
在这篇文章里,我们介绍了PoW并分析得到了实现PoW的基础方案;然后我们分析了ethash模块的实现方案,重点分析了ethash动态调整Header.Difficulty的方式和演变,以及使用巨大dataset计算有效哈希的方法。这篇文章主要是理论分析,在下篇文章中,我们将看看ethash的具体代码实现。
文章中若有不正确的地方,还请不吝指正。