引言
这是本博客中第一篇介绍数据结构与算法的文章,所以开头我想多说几句。算法是程序员「恰饭」的根本之一,这个无需多讨论。而这个东西偏偏又短时间难以掌握,所以如果平时不花点工夫进行学习,等用到了就抓瞎了。正所谓「人无远虑,必有近忧」。有人会说这些东西工作中用不到,我觉得可能还是没有真正的意识到一些东西,导致工作中即使接触到了,也不当回事。
不过话说回来,对于我来说学习算法不是为了参加竞赛,不是为了过某次面试。我学习算法想要以实用为主,同时开拓自己的思路,遇到问题时可以快速地想到更多解决方案。因此文章里(包括本篇)的一些描述和用词,可能并不专业,而是怎么方便理解怎么来。关于这一点还请读者了解。
本篇文章里我们介绍一下B树。「B树」这个名字是这个算法的发明人给起的,维基百科上介绍发明人没有解释字母「 B 」代表什么,可能是发明人之一 拜尔( Bayer )名字的首字母,也可能是当时所在的公司 Boeing 的首字母。不过我自己理解,代表「 Block 」也挺有意义的,具体原因看完这篇文章,你就明白了。
什么是B树
我们首先尝试着定义一下什么是B树。不过这种定义一般都很难理解,所以这里我们首先形象的看一下B树一般长什么样子,然后说明一下它的一些关键特性,最后再给出相对严谨的定义描述。
下面是一棵B树示意图(注意图中并没有示意出 key 所对应的 value 数据):

可以看到,与我们常见到的二叉树或红黑树不同,B树的每个结点中可以有多个 key。在上图中最多有 4 个,最少 2 个(这不是巧合,因为B树的每个结点内部必须有至少一半的有效的 key)。key 的排序倒与二叉树类似:某个 key 的左子树上的所有 key 都比自己小;右子树上的 key 都比自己大。
另外细心的你可能已经发现,上面这棵B树的所有叶子结点的高度都是一样的。这不是巧合,而是B树的操作规则导致它的所有叶子始终在同一高度上。
(不得不说的是,这个图中结点最大关键字数量并不严格符合B树的定义,在《算法导论》中要求B树中的最大关键字数量是一个奇数,因为这样一来有些操作就比较方便了。不过限于图片的展示大小,我这里暂时忽略了这一点,用了 4 个关键字而非 5 个)
看到这里,读者应该对B树有了一个大体的印象,但可能心里仍会有疑问:好像也没什么特别的,不过是每个结点的 key 多一些,叶子始终在同一高度上;但真是要查找某个 key,感觉好像还不如平衡二叉树方便呢(因为不光要在结点之间查找,还要在结点内部使用二分查找法查找);效率也不见得比红黑树或平衡二叉树高。
要解释这些疑问,要从各种树的应用场景说起。平衡二叉树(或红黑树)的应用虽然很多,但一般都是用来引用内存中的数据,即这些树的结点数据都在内存中;而B树一般应用在数据库索引或文件系统中,它引用的数据要大得多,多数结点数据都是存放在硬盘中的,而硬盘的访问速度显然比内存慢得多。这就显现出了B树的优势:同样的数据,如果使用B树组织,访问数据时需要读取磁盘的次数远小于使用平衡二叉树或红黑树时的访问次数。
比如如果要访问 key 为 45 的数据,在上面B树的例子中只需访问两次磁盘(根结点始终在内存中);而使用平衡二叉树最好的情况下也需要访问 4 次磁盘。并且这种差距会随着数据量的增加而更加明显。
所以B树的设计不仅仅是每个结点 key 多一些这么简单,它有自己的应用场景,那就是当数据大到需要将多数结点放到磁盘中时,B树既可以保证快速找到想要的数据,又可以保证访问磁盘的次数最少,从而最大化访问速度。
磁盘中有「块」(或「页」)的概念,「块」是磁盘每次访问的最小单位。也就是说,即使你只想读一个字节,也需要先从磁盘读上一个「块」的数据。所以对于多数结点都存储在磁盘上的B树来说,一个结点正好占用一个磁盘块(或至少一个)是最自然不过的了;而每个结点中最多有多少 key/value 数据对,则要看这些数据对的大小,并不是固定的。
所以我们可以总结B树有以下特点:
- 主要应用于数据库索引或文件系统中,所组织的数据和树结点本身多数位于磁盘上,而不是内存中。
- 每个结点的大小正好等于一个(或多个)磁盘块的大小
- 每个结点内部有多个 key/value 数据对,数据对的最大数量等于单个结点所能容纳的数据对的最大量;最小数量为最大数量的一半(根结点除外)
- 每个结点内部的 key 都有对应的左右子树;所有左子树中的 key 都小于自己;所有右子树的 key 都大于自己。
- 所有叶结点的高度是一样的
相信现在你已经对B树有了一个大致上的印象。在这一小节的最后,我们给出B树的严谨的定义。不过我觉得一件东西如何定义的不重要,它在你心中是什么样子才重要。
下面是《算法导论》一书中给出的B树的定义(我替换了书中使用的符号,我觉我的写法对于程序员来说更容易理解,虽然理解原书使用的符号也不难):
一棵B树 $T$ 是具有如下性质的有根树(根为 $root[T]$ ):
- 每个结点 node 有以下域:
a) node.count: 当前存储在结点 node 中的 key 的数量
b) node.key: 存放关键字的数组,一共 node.count 个,以非降序存放。所以 node.key[0] <= node.key[1] <= … <= node.key[node.count-1]
c) node.isLeaf: 一个布尔值,如果 node 是叶子的话,值为 true;否则为 false
d) node.child: 子结点数组,每个元素指向某个子结点。一共node.count+1个- 各关键字 node.key[i] 对储存在各子树中的关键字范围加以分隔:如果 $k_i$ 为存储在以 node.child[i] 为根的子树的关键字,则 $k_0$ <= node.key[0] <= $k_1$ <= node.key[1] <= … <= node.key[node.count-1] <= $k_{node.count}$
- 每个叶结点具有相同的高度,即树的高度 $h$
- 每一个结点能包含的关键字数有一个上界和下界。这个界称为B树的最小度数,我们使用固定整数 $t$ >= 2 来表示
a) 每个非根结点必须至少有 $t-1$ 个关键字,也即每个非根内结点至少有 $t$ 个子女。如果树是非空的,根结点至少包含一个关键字。
b) 每个结点可包含至多 $2t - 1$ 个关键字。所以一个内结点至多可有 $2t$ 个子女(如果恰好有 $2t - 1$ 关键字,我们就说这个结点是 「满的」)
这就是B树的定义。这里有几个要点,我们再次总结重申一下:一是B树的每个非根结点都有多个关键字(至少 $t-1$,至多 $2t-1$)和相应数量的子女;二是每个叶结点的高度相同。
在我刚看《算法导论》时,我感觉这里树的度数 $t$ 的定义稍显别扭:为什么要定义一个最小度数 $t$ 呢?无非就是结点关键字数量的上界和下界,直接定义每个结点最多有 $x$ 个、最少有 $\frac{x}{2}$ 个关键字,或最少有 $x$ 个、最多有 $2x$ 个关键字,不是也可以吗?其实书中这样定义的目的,是为了始终保证每个满结点有奇数个关键字,这一特点在「分裂结点」时特别有用。具体在后面介绍结点分裂时,再作详细的说明。
另外你会发现,当 $t = 1$ 时,每个结点最多有一个关键字、两个子女。这时的B树是最简单的,基本上等同于二叉树了。
在后面的介绍B树的各种操作时,我们仍会使用这个定义里出现的一些符号,请确保到目前为止理解了这些符号的含义。
B树的操作
下面我们来看看在B树上如何进行操作。对于多数数据结构,所进行的操作无非就是「增删改查」。「修改」这一操作是建立在其它操作的基础之上的,因此没什么可说的。这里我们重点关注查找、插入和删除。
在详细介绍插入和删除操作算法之前,我们需要记住B树的这俩操作的关键动作,它们就是:
分裂
合并
挪用
前两个关键动作是对于结点来说的,即「分裂结点」或「合并结点」;后一个是对关键字来说的,即「挪用关键字」。当在插入或删除过程中,被修改的结点不符合B树的要求时,我们就使用这三个关键操作中的一个对其进行处理,就可以使结点重新符合B树的要求。确切的说,当对某个结点进行「插入」或「删除」操作时,如果结点关键字的数量不再满足要求(至少 $t-1$,至多 $2t-1$),就需要对结点进行分裂或合并,或从别处挪用一个关键字过来。具体细节我们后面再说。
(我不确定这里用「关键动作」这一词语是不是准确,不过对于很多数据结构的操作算法来说,都有这样一类操作,比如红黑树的关键动作是「旋转」。对于这种数据结构,如果修改后不符合自身的要求,只要使用它的关键动作想办法调整一下,就可以重新符合要求。我觉得这是理解这类数据结构的操作算法的关键,并不需要死记硬背,希望读者能花心思体会一下。)
下面我们就详细说明一下针对B树的各种操作。在这个过程中,我们采用两个约定:
- B树的根始终在内存中。
- 除根以外,其它结点都在磁盘中。
基于这两个约定,在操作时B树的结点时,我们需要注意:
- 对非根结点进行操作之前,要先调用
DISK-READ将结点数据读取到内存中 - 对根结点进行操作之前无需调用
DISK-READ - 所有结点被修改后,要立即调用
DISK-WRITE将其写回磁盘 - 某个结点被删除,调用
DISK-DELETE将其从磁盘中删除
另外需要说明一点的是,与《算法导论》保持一致,我们这里对B树进行操作时,也只会沿着树的根下降,不会有任何结点的回溯。
查找
对于任意类型的树来说,查找操作是最简单的了,B树也是这样。相信不需要介绍,读者也知道该怎么查找(或称为「遍历」)一棵B树。与普通树(如二叉树)不同的是,B树在每个结点上不仅仅有两个分支,而是有多个分支。准确的说,如果一个结点有 n 个 key,那么在这个结点上就有 n+1 个分支,在进行查找时,需要对这 n 个 key 进行一个查找(如二分查找),来决定应该走哪个分支。
下面我们是查找B树的伪代码:
BTREE-SEARCH(root, k) {
// 找出使 k <= root.key[i] 成立的最小下标 i
// 注意如果没找到,i 的值会被设置为 root.count,
// 恰好是最后一个子女的下标
i <- 0
while i < root.count and k > root.key[i]
i <- i + 1
// 找到了,返回
if i < root.count and k == root.key[i] {
return (root, i)
}
// 达到叶子结点,查找结束
if root.isLeaf
return NIL
else
// 在女子 root.child[i] 中查找 k
DISK-READ(root.child[i])
return BTREE-SEARCH(k, root.child[i])
}
这个伪代码中使用了递归查找关键字 k,调用方式为 BTREE-SEARCH($root[T]$, k)。伪代码比较简单,也有详细的注释,这里就不多解释了。
插入
让我们「拍脑袋」想想,如何向B树中插入关键字呢?首先我们要找到这个关键字应该插入到哪个结点中;找到了这个结点,就可以把这个关键字插入到 node.key 数组中的合适位置了。
不过稍等,我们之前说过,B树的每个结点最多有 $2t-1$ 个关键字。所以如果我们找到的这个结点的关键字个数小于 $2t-1$,那么非常棒我们直接把关键字插入到 node.key 中的合适位置就可以了;但如果这个结点中的关键字正好是 $2t-1$ 个、即这是个满结点呢?此时是无法把这个关键字直接插入到这个结点中的。这时就要用到「分裂结点」这一关键动作了。那么什么是「分裂结点」呢?
结点的分裂
简单来说,分裂结点就是在向某个满结点插入新的关键字之前,先将这个满结点一分为二、变为两个结点的过程。变为两个结点之后,就有空间容纳新的关键字了。分裂之前的满结点有 $2t-1$个关键字;分裂后两个结点各有 $t-1$ 个关键字(其中前一个结点保留了原满结点比较小的 $t-1$ 个关键字;而后一个结点保留了原满结点比较大的 $t-1$ 个关键字);位于中间的那个关键字则被提到了父结点中,作为两个结点的分隔关键字。
注意刚才描述的分裂过程中,关键字数量一直保持不变:分裂前的满结点关键字数量为 $2t-1$,分裂后关键字数量为 $(t-1) + (t-1) + 1 = 2t-1$。另外这里也清楚的说明了《算法导论》中为什么要如此定义 $t$:满结点的关键字个数为 $2t-1$,这肯定是个奇数,因此分裂时总能保证每个新结点都有相同的、B树所要求的最少数量的 $t-1$ 个结点,同时也总能保证肯定有一个中间关键字可以被放到父结点中,用来分隔这两个新结点。
这一分裂的过程可用如下示意图表示:
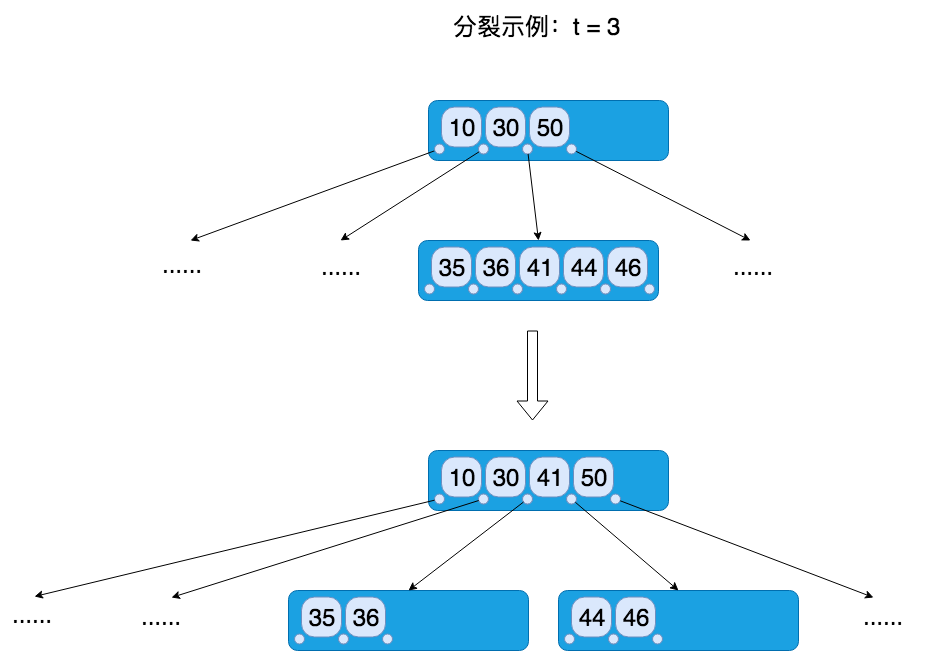
还需说明一点的是,分裂时可以将中间关键字放到父结点用来分隔两个新结点的前提条件是,父结点不是满结点。如果是父结点也是满结点该怎么办呢?
这里有两个办法,一个是继续向上分裂父结点,如果祖父结点也是满的,继续向上分裂,直到遇到一个非满的父结点。如果一路分裂到根结点,发现根结点也是满结点,那就只能分裂这个根结点,并新生成一个新结点作为根结点,而旧的根结点分裂而成的两个结点作为新根的两个子结点。这时树的高度增加了 1。
另一个办法是在从根开始下降查找将要插入的结点时,遇到满结点就将其分裂。这样一路找一路分裂下来,最后插入前进行分裂时,其父结点肯定不是满结点,因而可以正常分裂了。同第一个办法一样,如果根是满结点,树的高度也会加1。
第二个办法相对简单,《算法导论》中使用的就是这个方法,这里我们也使用这个方法。
这里顺便解释一下为什么B树的所有叶子结点高度都相同,且等于树的高度。从上面的两个方法可以看出,无论哪个方法,树的高度的增加都是由分裂根结点引起的,而不是像其它树结构那样,由新加入一个叶子结点引起的。因此B树的所有叶子总有相同的高度。
下面给出结点分裂的伪代码:
// BTREE-SPLIT 将一个指定的结点分裂成两个。
// parent: 将要分裂的结点(即 splitedNode)的父结点
// childIndex: 将要分裂的结点在 parent.child 中的下标值
// splitedNode: 将要被分裂的结点
BTREE-SPLIT(parent, childIndex, splitedNode) {
// splitKey 代表将被提取到 parent 中分隔两个分裂结点的关键字
splitKey <- splitedNode.key[t-1]
// 首先创建一个新的结点,并填充新结点的各个字段
// 这里我们把 splitedNode 中的后半部分的 key 和 child 放到 newNode 中
newNode <- ALLOC-NODE()
newNode.count <- t - 1
newNode.isLeaf <- splitedNode.isLeaf
for i <- 0 ; i < t-1 ; i++
newNode.key[i] <- splitedNode.key[i + t]
if not newNode.isLeaf
for i <- 0 ; i < t ; i++
newNode.child[i] <- splitedNode.child[i + t]
// 修改 splitedNode,只保留前半部分的 key 和 child
splitedNode.count <- t - 1
// 修改 parent,将分裂后的两个结点及新的 key 放到正确的位置
keyIndex = childIndex
for i <- parent.count; i > keyIndex; i--
parent.key[i] <- parent.key[i-1]
for i <- parent.count + 1; i > childIndex + 1; i--
parent.child[i] <- parent.child[i-1]
parent.key[keyIndex] <- splitKey
parent.child[childIndex + 1] <- newNode
parent.count <- parent.count + 1
DISK-WRITE(parent)
DISK-WRITE(splitedNode)
DISK-WRITE(newNode)
}
这段伪代码可以用如下示意图表示:
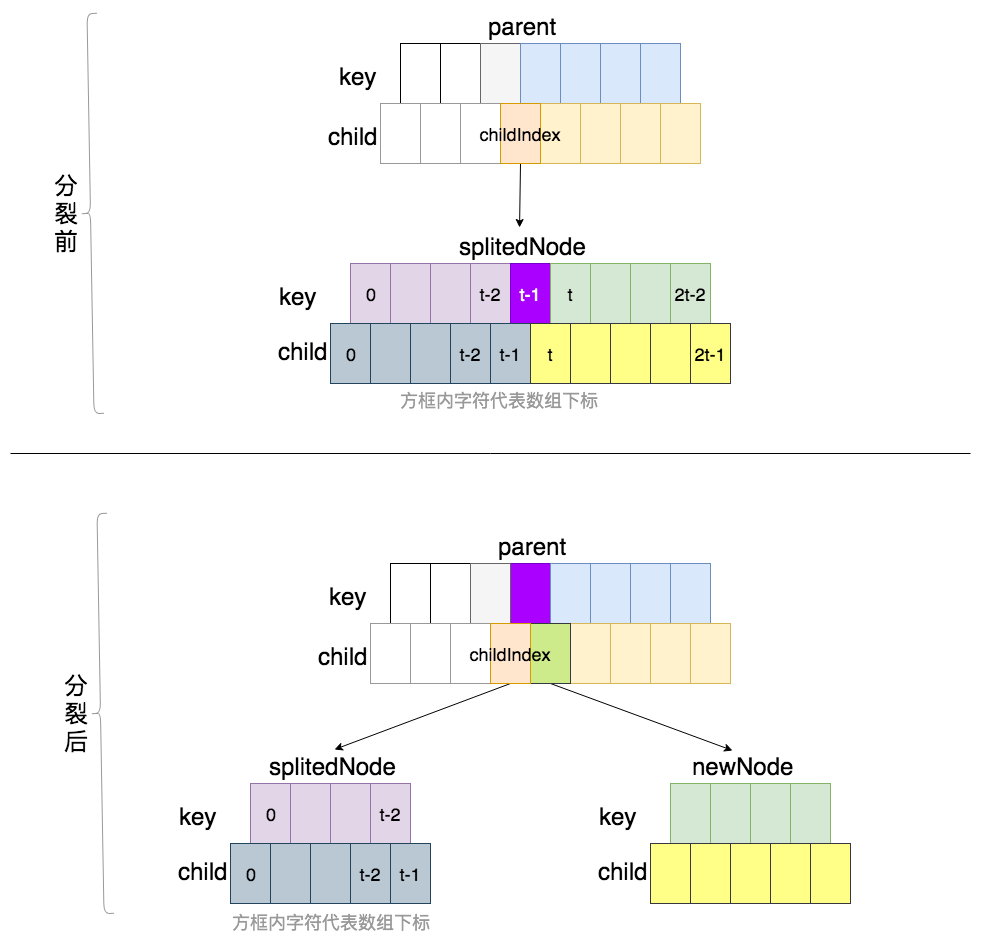
无回溯方式插入关键字
知道了如何分裂一个结点,整个插入过程就简单多了。这里我们使用的方法与《算法导论》中的一致,即无回溯的方式插入。
前面我们说过,分裂时有可能父结点也是满结点,有两个方法可以解决这个问题:一个是先递归向上分裂父结点,直到遇到一个非满的父结点,这种方式需要进行回溯;另一个是从根开始定位将要插入的结点时,每当遇到满结点就将其分裂,这种方式不需要进行回溯。这两种方法各有优劣,第一种方法实现起来稍复杂,但只有在必要时才会分裂结点,可以保持结点数量最小化;第二种方法实现起来比较简单,但有些满结点可能暂时不需要分裂,也会被分裂,使结点数量有一点点增大。这里我们使用的是第二种方法。
下面我们给出插入的伪代码:
BTREE-INSERT(T, k) {
r <- root[T]
if r.count == 2t-1 {
// 如果根结点是满的,首先分裂根结点
newR <- ALLOC-NODE()
newR.isLeaf <- false
newR.count <- 0
newR.child[0] <- r
root[T] <- newR
BTREE-SPLIT(newR, 0, r)
r <- newR
DISK-WRITE(r)
}
BTREE-INSERT-NONFULL(r, k)
}
// 注意 参数 node 总是非满的
BTREE-INSERT-NONFULL(node, k) {
// 找到 k 在 node 结点中的位置
i < - 0
while i < node.count and k > node.key[i]
i <- i + 1
// k 已经存在了,简单起见这里直接返回。
// 但也可能需要更新 k 所对应的值
if i < node.count and k == node.key[i]
return
if node.isLeaf {
// 如果 node 是叶结点,则将 k 插入其中
for j <- node.count; j > i; j <- j + 1
node.key[j] <- node.key[j - 1]
node.key[i] <- k
DISK-WRITE(node)
} else {
// 如果 node 是内部结点,则将 k 插入到合适的子结点中
child <- node.child[i]
DISK-READ(child)
// 如果这个合适的子结点是个满结点,则先对其进行分裂。
// 分裂后新提上来的关键字占据了 i 所指向的位置,因此
// 要判断一下,如果 k 大于新提上来的关键字,则子结点应
// 使用分裂时新创建的结点;否则仍为原来的子结点。
if child.count == 2t - 1 {
BTREE-SPLIT(node, i, child)
if k > node.key[i] {
child <- node.child[i + 1]
}
}
// 递归在子结点中插入 k
BTREE-INSERT-NONFULL(child, k)
}
}
插入的过程分成了两个函数,BTREE-INSERT 作为最顶层的函数,用来对B树的根进行分裂;输助函数 BTREE-INSERT-NONFULL 执行真正的插入动作。注意它的参数 node 所代表的永远是一个非满的结点。
删除
现在我们再来看看删除操作。B树的删除操作要比插入操作复杂得多,但不要紧张,只要理清了逻辑,复杂的问题也会变得很简单。
我们依然「拍脑袋」想想要删除一个B树中的关键字,需要怎么做。首先我们要找到关键字所在的位置,找到以后将这个关键字「去掉」就好了。
这里的「去掉」是有技巧的。不同能类型的结点,「去掉」的方法也不一样:
在叶结点中:把后续的关键字向前移动,覆盖掉要删除的那个关键字
在内结点中:不能使用叶结点中移动覆盖的方法,而要用其它关键字「替换」将被删除的关键字
这里先简单说一下在内结点中删除关键字时的情形。其实在内结点中删除关键字,需要用内结点的子树中的最值(左子树的最大值,或右子树的最小值)替换。替换时需要先将这个最值删掉,然后再用这个最值替换掉要删除的关键字。你可能会想到,这个最值肯定是在子树地叶子结点中,不是吗?如此一来,在内结点中删除关键字的问题,也转变成在叶结点中删除关键字的问题了。
所以现在「去掉」关键字的方法的关键只有一个:
在叶结点中:把后续的关键字向前移动,覆盖掉要删除的那个关键字
这一方法看似简单,其实有一个重要问题需要解决,那就是在叶结点中删除关键字时,我们要保证「去掉」一个关键字后,B树仍然能保持它的性质不变,即所有结点的关键字数量仍然不小于 $t-1$。例如在一个只有 $t-1$ 个关键字的叶结点中,你不能直接删除结点中的某个关键字。
如何解决这个问题呢?很自然的我们会想,只要保证在删除前,叶结点中的关键字数量大于 $t-1$ 就可以了。那么如何保证呢?这里也有两个方法:
如果任一兄弟结点关键字数量大于 $t-1$,就使用
方法1:从兄弟结点中「挪」一个关键字过来
如果所有兄弟结点的关键字数量都为 $t-1$,就使用
方法2:将两个兄弟结点「合并」,组成一个拥有 $2t-1$ 个关键字的新结点
但是新的问题又出现了。方法2 中「合并」两个兄弟结点时,需要从父结点取走一个关键字。如果父结点也只有 $t-1$ 关键字该怎么办呢?我们要保证合并前,父结点的关键字数量也大于 $t-1$ ……
好像问题的解决方案开始递归了,不过可以看到,「挪」关键字和「合并结点」这两个方法,是保证任意一个结点(内结点和叶结点)的关键字数量大于 $t-1$ 的通用方法。(文章前面提到过的「关键动作」,也包含了这两种方法)。只要能保证某个结点是非最小结点,就可以从中删除关键字了。
这一段描述到现在,已经全部解决了删除B树关键字这一操作的几乎所有问题。我们再整理一下这里面的关键问题:
- 如何删除内结点中的关键字
- 关键:删除子树叶结点中的关键字
- 如何删除叶结点中的关键字
- 关键:保证叶结点和父结点(内结点)的关键字数量大于 $t-1$
- 如何从兄弟结点中「挪」一个关键字到自己结点中
- 如何「合并」两个兄弟结点
- 关键:保证叶结点和父结点(内结点)的关键字数量大于 $t-1$
只要我们从解决掉上面这棵「问题树」,B树的删除问题就可以解决了。我们下面会对这里面的所有关键进行详细的说明。(如果不是十分理解上面这一段的描述也没关系,等看完详细介绍再回过头来看这一段描述,应该会有一个更加整体和深刻的印象)
从兄弟中挪用关键字
从兄弟中挪用关键字,即将某个兄弟的关键字减小一个,而将自己的关键字增加一个。以下是这一操作的示意图(图中展示的是从左兄弟中挪用关键字,从右兄弟中挪用与之类似,就不再展示了):
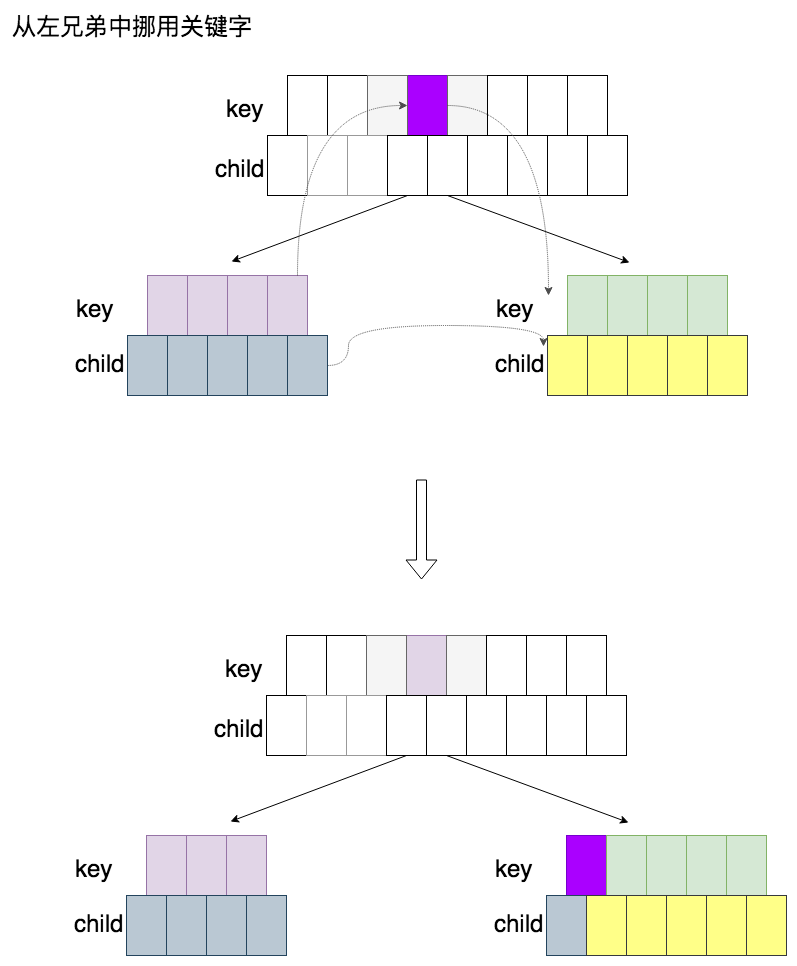
从图中可以看出,其实严格来说不是直接从兄弟中挪用,而是先将父结点中分隔兄弟俩的关键字挪到自己结点中,再将兄弟的关键字挪到父结点中作为新的分隔兄弟俩的关键字。
下面是这一操作的伪代码:
// BTREE-EXTEND-FROM-LEFT-BROTHER 从左兄弟中挪一个关键字到自己结点中
// parent: 将要增加关键字的结点的父结点
// childIndex: 将要增加关键字的结点在 parent.child 中的下标索引
// node: 将要增加关键字的结点
BTREE-EXTEND-FROM-LEFT-BROTHER(parent, childIndex, node) {
leftBrotherIndex <- childIndex - 1
leftBrother <- parent.child[leftBrotherIndex]
// 移除左兄弟的最大的关键字及其右孩子
newSplitkey, child <- BTREE-REMOVE-MAX-IN-NODE(leftBrother)
// 将旧的分隔关键字及 child 加入到自己结点中
// 然后并新的分隔关键字写入 parent 中
splitkeyIndex <- leftBrotherIndex
BTREE-INSERT-AS-MIN-IN-NODE(node, parent.key[splitkeyIndex], child)
parent.key[splitkeyIndex] <- newSlitKey
DISK-WRITE(parent)
}
// BTREE-EXTEND-FROM-RIGHT-BROTHER 从右兄弟中挪一个关键字到自己结点中
// parent: 将要增加关键字的结点的父结点
// childIndex: 将要增加关键字的结点在 parent.child 中的下标索引
// node: 将要增加关键字的结点
BTREE-EXTEND-FROM-RIGHT-BROTHER(parent, childIndex, node) {
rightBrotherIndex <- childIndex + 1
rightBrother <- parent.child[rightBrotherIndex]
// 移除右兄弟的最小关键字及其左孩子
newSplitkey, child <- BTREE-REMOVE-MIN-IN-NODE(rightBrother)
// 将旧的分隔关键字及 child 加入到自己结点中
// 然后并新的分隔关键字写入 parent 中
splitKeyIndex <- childIndex
BTREE-INSERT-AS-MAX-IN-NODE(node, parent.key[splitKeyIndex], child)
parent.key[splitKeyIndex] <- newSplitKey
DISK-WRITE(parent)
}
这里共两个函数,分别用来从左兄弟和右兄弟中挪用关键字。这两个函数都比较简单,就不多解释了。其中用到了几个辅助函数,它们的伪代码如下:
// BTREE-INSERT-AS-MIN-IN-NODE 将 key 和 child 作为最小关键字
// 写入 node 结点中
BTREE-INSERT-AS-MIN-IN-NODE(node, key, child) {
for i <- node.count; i > 0; i <- i - 1
node.key[i] <- node.key[i - 1]
if not node.isLeaf
for i <- node.count + 1; i > 0; i <- i - 1
node.child[i] <- node.child[i - 1]
node.key[0] <- key
if not node.isLeaf
node.child[0] <- child
node.count <- node.count + 1
DISK-WRITE(node)
}
// BTREE-INSERT-AS-MAX-IN-NODE 将 key 和 child 作为最大关键字
// 写入 node 结点中
BTREE-INSERT-AS-MAX-IN-NODE(node, key, child) {
node.key[node.count] <- key
if not node.isLeaf
node.child[node.count + 1] <- child
node.count <- node.count + 1
DISK-WRITE(node)
}
// BTREE-REMOVE-MAX-IN-NODE 将 node 中
// 最大的关键字及其右孩子移除,并返回
BTREE-REMOVE-MAX-IN-NODE(node) {
key <- node.key[node.count - 1]
if not node.isLeaf
child <- node.child[node.count]
else
child <- NIL
node.count <- node.count - 1
DISK-WRITE(node)
return (key, child)
}
// BTREE-REMOVE-MIN-IN-NODE 将 node 中
// 最小的关键字及其左孩子移除,并返回
BTREE-REMOVE-MIN-IN-NODE(node) {
key <- node.key[0]
if not node.isLeaf
child <- node.child[0]
else
child <- NIL
for i <- 0; i < node.count - 1; i <- i + 1
node.key[i] <- node.key[i+1]
if not node.isLeaf
for i <- 0; i < node.count; i <- i + 1
node.child[i] <- node.child[i+1]
node.count <- node.count - 1
DISK-WRITE(node)
return (key, child)
}
合并结点
刚才我们介绍的从兄弟中挪用关键字的前提是,兄弟中有关键字可以挪用,即左右两兄弟中至少有一个关键字数量大于 $t-1$。但如果某结点左右两兄弟的关键字数量都为 $t-1$ 该怎么办呢?那只能合并结点了。
所谓合并结点,就是将两个关键字数量为 $t-1$ 的结点合并为一个结点,加上父结点中的分隔关键字,新结点的关键字数量正好为 $2t-1$。下面是这一操作的示意图:
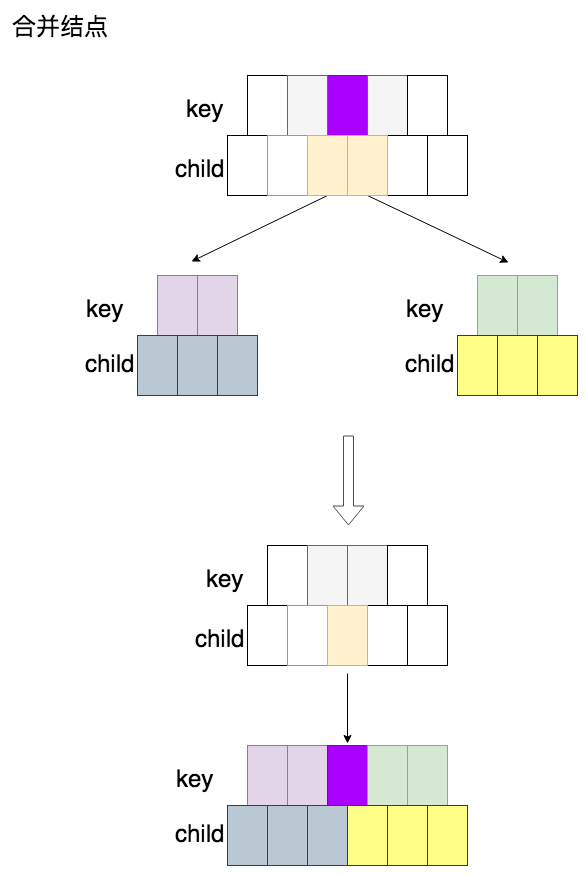
这里需要特别强调的一点是,两个结点可以合并,除了两个结点的关键字数量都必须为 $t-1$ 外,还有一个重要的前提是父结点的关键字数量大于 $t-1$。因为合并时将把分隔关键字从父结点中移除,放入新结点中,这会导致父结点的关键字数量减 1。如果合并时父结点的关键字数量为 $t-1$,合并后父结点就不符合B树的要求了。
下面是合并这一过程的伪代码如下:
// BTREE-MERGE-NODE 合并 parent 中由 splitKeyIndex 索引的
// 关键字作为分隔关键字的两个子结点。
// parent: 将要合并的两个结点的父结点
// splitKeyIndex: 将要合并的两个结点的分隔关键字在 parent.key 中的索引
// leftNode: 将要被合并的左结点
// rightNode: 将要被合并的右结点
BTREE-MERGE-NODE(parent, splitKeyIndex, leftNode, rightNode) {
// 简单起见,新结点我们直接复用左孩子,
// 这样就不用再拷贝左孩子中的数据到 newNode 中了。
newNode <- leftNode
// 将父结点中的分隔关键字放到 newNode 中
newNode.key[leftNode.count] <- parent.key[splitKeyIndex]
// 将右子结点中的关键字和 child 拼接到 newNode 中
// 已有的关键字和 child 后面
for i <- 0; i < rightNode.count; i <- i + 1
newNode.key[leftNode.count + 1 + i] <- rightNode.key[i]
if not rightNode.isLeaf {
for i <- 0; i < rightNode.count + 1; i <- i + 1
newNode.child[leftNode.count + 1 + i] <- rightNode.child[i]
}
// 设置新结点的叶子标志和关键字数量。
// 到此新结点完全创建成功。
newNode.isLeaf <- leftNode.isLeaf
newNode.count <- leftNode.count + rightNode.count + 1
// 现在 newNode 已经初始化完毕,下面要修改父结点,
// 一是把原来的分隔关键字抹掉;
// 二是把 newNode 放入 parent 中的合适位置(即取代 leftNode 的位置)
for i <- splitKeyIndex; i < parent.count - 1; i <- i + 1
parent.key[i] <- parent.key[i + 1]
for i <- splitKeyIndex + 1; i < parent.count; i <- i + 1
parent.child[i] <- parent.child[i + 1]
parent.child[splitKeyIndex] <- newNode
parent.count <- parent.count - 1
DISK-WRITE(newNode)
DISK-WRITE(parent)
// 由于 newNode 复用的 leftNode,所以这里不要删除 leftNode
DISK-DELETE(rightNode)
}
这段代码虽然稍长,但逻辑比较简单,就不再多作解释了。
确保结点为非最小结点
刚才我们说了,两个结点可以合并的前提之一,是父结点的关键字数量大于 $t-1$,即父结点不能是最小结点。但如果父结点是最小结点,又需要合并其中两个子结点,该怎么办呢?
其中一个办法是先把父结点变成非最小结点,这可以通过对父结点使用前面我们已经介绍过的挪用关键字或合并结点的方式实现;而在这个过程中如果将父结点与它的兄弟结点合并的情况,我们又需要保证父父结点为非最小结点。
可以看到,这是个方法需要回溯父结点。还记得在插入操作中,我们使用了非回溯的方式进行插入,即在从根结点开始查找插入位置时,每遇到一个满结点,我们就将其分裂,变成非满结点。类似的,在删除时我们也可以使用非回溯的方式。
使用非回溯的方式删除关键字时,我们从根结点开始查找要删除的关键字,每遇到一个最小结点,我们就想办法将其变成非最小结点。这样,当我们想要合并某两个兄弟结点时,它们的父结点肯定不会是最小结点,也就符合合并的要求了。
这里的关键是「想办法将结点变成非最小结点」。其实使用前面我们介绍过的两种方式:关键字挪用和合并,就可以让任何一个结点变成非最小结点。由于主要方法前面已经介绍过了,这里就不再画示意图了,直接看伪代码就行了:
// BTREE-ENSURE-NON-MINNODE 确保指定的结点为非最小结点。
// 它会将代替 node 的非最小结点返回,
// 这个新的结点有可能是 node,也可能不是。
// parent: 要确保的结点的父结点
// nodeIndex: 要确保的结点在 parent.child 中的索引
// node: 要确保为非最小结点的结点
BTREE-ENSURE-NON-MINNODE(parent, nodeIndex, node) {
if node.count > t - 1
return node, nodeIndex
// 根结点的关键字数量可以小于 t-1,所以永远不是最小结点
if parent == NIL
return node, nodeIndex
// node 是一个最小结点,下面的操作要让它变成一个非最小结点
// 首先尝试从左兄弟中挪一个关键字
leftBrother <- parent.child[nodeIndex - 1]
DISK-READ(leftBrother)
if nodeIndex > 0 and leftBrother.count > t - 1 {
BTREE-EXTEND-KEY-FROM-LEFT-BROTHER(parent, nodeIndex, node)
return node, nodeIndex
}
// 尝试从右兄弟中挪一个关键字
rightBrother <- parent.child[nodeIndex + 1]
DISK-READ(rightBrother)
if nodeIndex < child.count and rightBrother.count > t - 1 {
BTREE-EXTEND-KEY-FROM-RIGHT-BROTHER(parent, nodeIndex, node)
return node, nodeIndex
}
// 左右兄弟都无法挪关键字,好合并了
// 这里注意合并后新结点在 parent.child 中的索引
if nodeIndex != 0 {
// 左兄弟存在,跟左兄弟合并
BTREE-MERGE-NODE(parent, nodeIndex - 1, leftBrother, node)
node <- parent.child[nodeIndex - 1]
nodeIndex <- nodeIndex - 1
} else {
// 没有左兄弟,只能跟右兄弟合并
BTREE-MERGE-NODE(parent, nodeIndex, node, rightBrother)
node <- parent.child[nodeIndex]
}
return node, nodeIndex
}
可以看到这个函数基本是将前面挪用关键字和合并结点两个操作结合了起来:如果可以通过挪用关键字的方式保证结点为非最小结点,就优先挪用关键字;否则就合并。
叶结点中删除关键字
在叶结点中删除关键字比较简单,按照前面说的,只要把后续的关键字向前移动,覆盖掉将要删除的关键字就可以了。但前提是必须保证叶结点的不是最小结点。
删除过程比较简单,我们就不用示意图了,直接看伪代码吧:
// BTREE-DELETE-KEY-IN-LEAF 用来删除叶子结点中的某个关键字。
// parent: 为叶子结点的父结点
// nodeIndex: 为叶子结点在 parent.child 中的下标索引
// node: 为包含将要删除关键字的叶子结点
// deletedKeyIndex: node.key 中将要删除的关键字的下标
// deletedKey: 为将要删除的关键字的值
BTREE-DELETE-KEY-IN-LEAF(parent, nodeIndex, node, deletedKeyIndex, deletedKey) {
// BTREE-ENSURE-NON-MINNODE 用来保证叶子结点 node 不是最小结点
deleteFromNode, _ <- BTREE-ENSURE-NON-MINNODE(parent, nodeIndex, node)
// BTREE-ENSURE-NON-MINNODE 返回的 deleteFromNode 可能
// 并不是 node,或者是 node 但关键字的索引已经发生了变化,
// 这里要对其进行修正。详细说明见伪代码后面的解释。
if deleteFromNode.key[deletedKeyIndex] != deletedKey
deletedKeyIndex <- deletedKeyIndex + 1
if deleteFromNode.key[deletedKeyIndex] != deletedKey
deletedKeyIndex <- deleteKeyIndex - 1 + t
// 向前移动,覆盖掉要删除的关键字
for i <- deletedKeyIndex; i < deleteFromNode.count - 1; i <- i + 1
deleteFromNode.key[i] <- deleteFromNode.key[i+1]
deleteFromNode.count <- deleteFromNode.count - 1
DISK-WRITE(deleteFromNode)
}
虽然在叶子结点中删除关键字比较简单,但我们要保证删除之前叶子结点为非最小结点,因此我们调用了 BTREE-ENSURE-NON-MINNODE 函数。这一调用就引出了麻烦:因为这个函数可能会让关键字的索引发生变化,所以我们调用后必须重新修正要删除的关键字所在的索引位置。
根据上一小节的介绍, BTREE-ENSURE-NON-MINNODE 函数可能会对 node 结点作以下操作:
- 没有任何操作,node 本来就是一个非最小结点
- 从右兄弟中挪一个关键字到 node 中
- 从左兄弟中挪一个关键字到 node 中
- 将 node 与左兄弟合并
- 将 node 与右兄弟合并
这五个操作中,只有第 3 和第 4 个操作会改变被删除关键字的位置,使得 deleteFromNode.key[deletedKeyIndex] != deletedKey。所以我们需要对这两种情况作修正,保证 deleteFromNode.key[deletedKeyIndex] == deletedKey 。
如果是第 3 种情况,新挪用的关键字会插入到 node.key[0] 的位置,而 node 中原来的关键字都会向右顺移一位,因此只要将索引值加1,就是 deletedKey 所在的位置。所以我们使用以下代码进行调整:
if deleteFromNode.key[deletedKeyIndex] != deletedKey
deletedKeyIndex <- deletedKeyIndex + 1
我们这里只是假设是第 3 种情况,所以这个调整不一定是对的。如果调整完了还不对,那就只能是第 4 种情况。这种情况下左兄弟中的 $t-1$ 个关键字以及父结点中的分隔关键字都被插入到了 node 结点中原关键字的前面,所以 node 中原有的关键字不是向右顺移了一位,而是 t 位。然而刚才处理第 3 种情况时我们已经向右移了一位了,所以要先恢复这一次移动,再向右移 t 位。这里使用以下代码进行调整:
if deleteFromNode.key[deletedKeyIndex] != deletedKey
deletedKeyIndex <- deleteKeyIndex - 1 + t
两次调整以后,deletedKeyIndex 中的关键字值肯定就是 deletedKey 了。注意如果不是第 3 或第 4 种情况,就根本不会进入这两个 if 分支中的任意一个。
相信这样解释一番以后,BTREE-DELETE-KEY-IN-LEAF 这个函数就更好理解了。其实这个函数里我们对关键字位置进行调整的代码,隐含了对 BTREE-ENSURE-NON-MINNODE 函数太多的假设,我们需要完全清楚 BTREE-ENSURE-NON-MINNODE 是怎么实现的,只要它有改动,我们这里的实现可能就要跟着改动,否则就会出错。这种问题可不是我们写代码的时候想见到的。其实这里还有一种处理方法,就是在 deleteFromNode 中重新查找关键在所在的位置,如下伪代码所示:
if deleteFromNode.key[deletedKeyIndex] != deletedKey {
deletedKeyIndex <- 0
while deleteFromNode.key[deletedKeyIndex] != deletedKey {
deletedKeyIndex <- deletedKeyIndex + 1
}
}
这样一来,只要 BTREE-ENSURE-NON-MINNODE 能实现自己声称的功能,我们完全不关心它是如何实现的。缺点就是效率稍低一点(相对而言,我觉得只要不是非常频繁的删除,差别不会太大,并且这里还可以用二分查找增加效率)。在实际应用中,我会更喜欢后一种实现。
内结点中删除关键字
下面我们来看看在内结点中如何删除关键字。由于内结点有自己的子结点,所以直接删除关键字的话,关键字作为子结点的分隔就会发生错乱。因此只能用别的关键字替换掉想要删除的关键字。那么用哪个关键字来替换呢?我们想一下,原来的关键字作为一个分隔关键字,它的值比左子树中的所有值都大,比右子树中的所有值都小。那么很自然的,左子树中的最大值或右子树中的最小值,都可以用来替换。
那么如何进行替换呢?简单来说,就是将左子树的最大值或右子树的最小值删掉,然后用这个最值覆盖掉我们想删除的关键字就可以了。而左子树的最大值或右子树的最小值肯定都在叶结点上,将这个最值删掉相当于从叶结点中删除一个关键字,这个我们上一小节已经说过了。
一般而言删除左子树的最大值比删除右子树的最小值简单一点(最大值的删除只需将 node.count 减 1 即可,而最小值的删除需要将 node.key[0] 后面的元素都向前移动一下),所以我们选择使用左子树的最大值来进行替换。下面是在内结点中删除关键字的示意图:
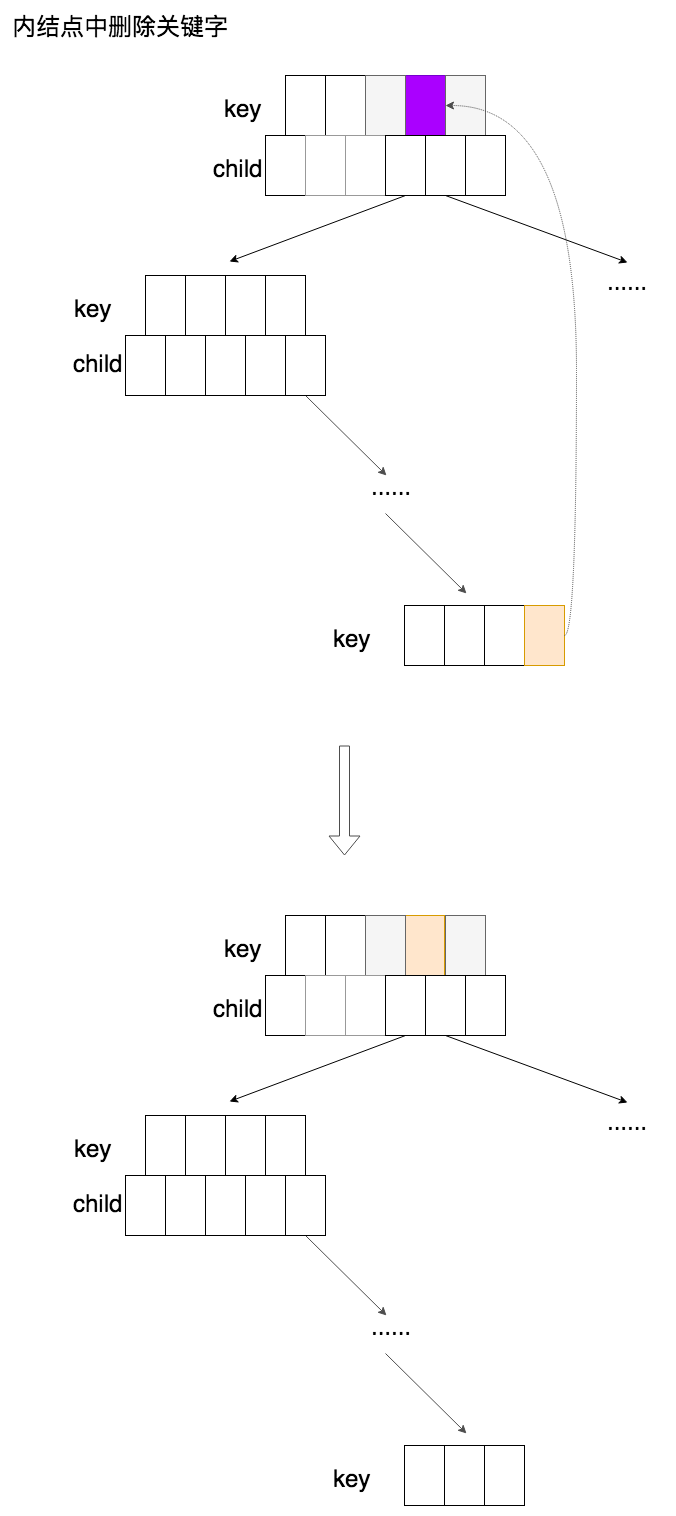
这个示意图显示了一种比较简单的情况,即在左子树中向下查找要删除的关键字时,没有发生任何挪用关键字或合并结点的时候,且存放左子树最大关键字的叶结点也不是最小结点,可以直接删除这个关键字。比较复杂的情况是,在删除左子树最大值时,会一直进行结点合并,以至于删除了左子树的最大值以后,原本想要删除的关键子已经不在原来的结点中了,而是被合并操作合并到一个新的结点中了。
下面是在内结点中删除关键字的伪代码:
// BTREE-DELETE-KEY-IN-INNERNODE 删除一个内部结点的关键字。
// node: 想要删除的关键字所在的结点
// deletedKeyIndex: 想要删除的关键字在 node.key 中的索引
// deletedKey: 想要删除的关键字的值
BTREE-DELETE-KEY-IN-INNERNODE(node, deletedKeyIndex, deletedKey) {
newKey <- BTREE-GET-MAXKEY(node.child[deletedKeyIndex])
// 将左子树中的最大值删除
// 由于调用 BTREE-DELETE-WITH-NODE 时传入的第 3 个参数必须是
// 非最小结点,因此我们首先调用 BTREE-ENSURE-NON-MINNODE 保证这一点
leftChild, leftChildIndex <-
BTREE-ENSURE-NON-MINNODE(node, deletedKeyIndex, node.child[deletedKeyIndex])
BTREE-DELETE-WITH-NODE(node, leftChildIndex, leftChild, newKey)
// 删除左子树最大关键字后,原本要删除的关键字的位置可能就变了,
// 所以这里不能直接使用 deletedKeyIndex 索引要删除的关键字的位置,
// 而是要重新查找。
node, deletedKeyIndex <- BTREE-SEARCH(node, deletedKey)
node.key[deletedKeyIndex] <- newKey
DISK-WRITE(node)
}
这段代码用到了一个辅助函数 BTREE-GET-MAXKEY,用来获取子树的最大关键字的值。它的伪代码如下:
BTREE-GET-MAXKEY(root) {
if root.isLeaf
return root.key[root.count - 1]
DISK-READ(root.child[root.count])
BTREE-GET-MAXKEY(root.child[root.count])
}
非回溯删除
上面我们讨论了所有删除过程中遇到的问题和解决方法,现在可以将它们汇总起来,实现非回溯方式删除这一操作了。具体伪代码如下:
// BTREE-DELETE 删除B树 T 中的某个关键字。
BTREE-DELETE(T, k) {
BTREE-DELETE-IN-NODE(NIL, -1, root[T], k)
}
// BTREE-DELETE-WITH-NODE 删除以 node 为代表的子树中的关键字 k。
// 注意调用这个函数前,node 必须是一个非最小结点(除非它是根结点)。
BTREE-DELETE-WITH-NODE(parent, nodeIndex, node, k) {
// 查找关键字的合适位置
i <- 0
while i < node.count and k > node.key[i]
i <- i + 1
// 不可能有合适的位置存储这个关键字,返回
if i >= node.count
return
// 找到了,删除
if k == node.key[i] {
BTREE-DELETE-KEY(parent, nodeIndex, node, k, i)
return
}
// 没找着,但已经到了叶子结点了,不可能有了。返回
if node.isLeaf
return
// 没找着,继续在子结点中递归删除
// 但在继续查找之前,要保证 node.child[i] 不是最小结点
ENSURE-NON-MINNODE(node, i, node.child[i])
BTREE-DELETE-WITH-NODE(node, node.child[i], k)
}
// BTREE-DELETE-KEY 删除 node 结点中的关键字。
// 注意调用这个函数时,要删除的关键字肯定在 node 结点中。
BTREE-DELETE-KEY(parent, nodeIndex, node, deletedKeyIndex, deletedKey) {
if node.isLeaf
BTREE-DELETE-KEY-IN-LEAF(parent, nodeIndex, node, deletedKeyIndex, deletedKey)
else
BTREE-DELETE-KEY-IN-INNERNODE(node, deletedKeyIndex, deletedKey)
}
这段伪代码中有 3 个函数,它们基本就是把前面介绍的操作和问题解决方法串在了一起,因此这里就不再细说了。
总结
在这篇文章里,我们介绍了B树以及它的各种操作。B树多用于数据库索引或文件系统中,在这些环境中,几乎所有数据都存放在磁盘中,因此对数据访问时需要尽可能地减少对磁盘的访问次数。而B树的特性恰好可以在非常少的访问磁盘的情况下,进行各种操作。
B树的操作包含查找、插入、删除。每种树都有自己的「关键动作」,B树也不例外。B树的关键动作包含插入时的分裂结点,删除时的合并结点、挪用关键字等。只要理解了这些关键动作,就能深刻理解B树这种数据结构。
限于作者水平,文章中难免有错误的地方,如果发现感谢您能不吝指正。