• 1. 多个变量的一致性保证
• 2. 通用的转换
  • 2.1 例子
  • 2.2 乘法以外的转换
  • 2.3 为什么只能有加减
• 3. 新的证明过程
• 4. 总结
• 5. 附：矩阵的表示形式

在上一篇文章里，我们了解了如何将多个数学运算转换成多项式。但这个转换还有很多地方需要改进，这篇文章我们就来了解一下到底还有哪些问题、如何改进。

1. 多个变量的一致性保证

上篇文章里，我们有一个这样的例子：

我们知道了如何将这组运算用三个多项式 $l(x)$ 、$r(x)$ 和 $o(x)$ 表示。但我们稍微改变一下：

只是把原来的 $a_2$ 换成了 $a_1$ 。也就是说，现在第一个等式和第二个等式中，使用了同一个值。但是上一篇介绍的多项式转换的方法，在现在这个例子中，是没法保证 $a_1 = a_2$ 成立的。具体来说，现在我们想让 $l(x)$ 经过三个点 $(1, a_1), (2, a_1), (3,a_3)$ ，但之前的方法只能保证 $l(x)$ 经过点 $(1, a_1), (2, a_2), (3, a_3)$ ，这里 $a_2$ 是可以任意取值的，并不一定要等于 $a_1$ 。这种情况下，这个转换好像就不那么「等价」了。

你可能会问，那我们在转换的时候，就让 $l(x)$ 经过 $(1, a_1), (2, a_1), (3, a_3)$ 这三个点就好啦，这不就让 $x=1$ 时和 $x=2$ 时的值都是 $a_1$ 了嘛。但是别忘了，这个过程是 prover 来做的，prover 要这么做，要么能向别人证明 ta 确实令 $l(x)$ 在 $x=1$ 和 $x=2$ 时的值都是 $a_1$ ；要么需要让别人相信，ta 除了满足「 $l(x)$ 在 $x=1$ 和 $x=2$ 时的值都是 $a_1$」这个条件外，别无他法。

事实上，在保证「隐私」的情况下，向别人证明确实「令 $l(x)$ 在 $x=1$ 和 $x=2$ 时的值都是 $a_1$」很难，因为 $a_1$ 这个值及其运算其实就是零知识证明不能公开的「隐私数据」，如果都公开了，那别人是能验证了，但那也不是零知识证明了。所以这里选择了另一种方式，即让别人相信，prover 除了满足「 $l(x)$ 在 $x=1$ 和 $x=2$ 时的值都是 $a_1$」这个条件外，别无他法。

在具体执行的过程中，除了 prover ，没有人知道 $a_1$ 的值到底是多少（$a_1$ 代表的是程序执行过程中的变量，比如上一篇文章里的例子中，foo 函数的参数 a）。但我们都知道，它肯定是 1 的倍数。所以，我们令 $l(x)$ 经过点 $(1, 1), (2, 1), (3, a_3)$ 。然后在 prover 生成 proof 的过程中（这时 prover 已经知道 $a_1$ 的具体值了），将 $l(x)$ 乘以 $a_1$ 得到一个新的多项式 $l’(x)=a_1l(x)$ ，我们可以确认 $l’(x)$ 肯定经过了点 $(1, a_1), (2, a_1), (3, a_1a_3)$ 。这样一来，$a_1$ 的值只有 prover 知道，最终也能确认第一个等式和第二个等式的运算符左侧的值都是 $a_1$ （实际上只是看上去都是 $a_1$ ，这里并没有具体措施让 prover 必须这么干）。

但你肯定发现了，$l(x)$ 乘以 $a_1$ 后，第 3 个点 $(3, a_1a_3)$ 并不正确，我们原来只是想让 $l(x)$ 经过 $(3, a_3)$ 的。所以我们得另想办法，让 $l(x)$ 乘以 $a_1$ 后，不能影响第 3 个点。既然第 3 个点这么碍事，我们能不能直接把它从 $l(x)$ 中去掉完事呢？

答案肯定是可以的。我们把原来的 $l(x)$ 拆成两个多项式：$l_1(x)$ 和 $l_3(x)$ ，然后巧妙的选择这两个多项式经过的点，比如令：

• $l_1(x)$ 经过 $(1, 1), (2, 1), (3, 0)$ 这三个点
• $l_3(x)$ 经过 $(1, 0), (2, 0), (3, 1)$ 这三个点 注意看 $l_1(x)$ 和 $l_3(x)$ 经过的三个点的选点技巧和不同：在三个点中，有 $a_1$ 的地方，$l_1(x)$ 的值都是 1 ；在没有 $a_1$ 的地方，$l_1(x)$ 的值都是 0 。 然后我们可以使用 $a_1$ 、$l_1(x)$ 、$a_3$ 、$l_3(x)$ 构造一个最终的代表左侧的多项式 $L(x)$ ：

这样一来：

• $x=1$ 时，$L(1) = a_1l_1(1) + a_3l_3(1) = a_1 \cdot 1 + a_3 \cdot 0 = a_1$
• $x=2$ 时，$L(2) = a_1l_1(2) + a_3l_3(2) = a_1 \cdot 1 + a_3 \cdot 0 = a_1$
• $x=3$ 时，$L(3) = a_1l_1(3) + a_3l_3(3) = a_1 \cdot 0 + a_3 \cdot 1 = a_3$

是不是很巧妙？我们将每个变量都用一个多项式来表示，然后将它们合在一起构造 $L(x)$ 。通过巧妙的选择多项式经过的点，可以让最终的 $L(x)$ 跟我们上一篇文章里介绍，既能代表原来的操作数（也就是我们这篇里提到的变量，一个意思），也能保证在不同运算等式中，使用的同一个值（如 $a_1$）。

我们可以把 $l_1(x)$ 、$l_3(x)$ 这样的多项式叫做变量多项式（variable polynomials）。类似的，也有 $r_1(x)$ 和 $o_1(x)$ ，当然也有 $R(x)$ 和 $O(x)$ 代表最终的右侧多项式和输出多项式。

现在，我们即可以隐藏各个变量（$a_1$ 、$b_1$ 等），又可以让多项式能等价代表不同运算等式使用同一变量（如例子中 $a_1$ ）的情况。但仍然有一个问题，就是现在这种方式并不是强制的，prover 可以用上面我们介绍的方式生成 $L(x)$ ，也可以用其它方式。

前面我们提过，要解决这个问题，需要让别人相信，prover 除了满足「 $l(x)$ 在 $x=1$ 和 $x=2$ 时的值都是 $a_1$」这个条件外，别无他法。如何做到呢？我们依然可以利用之前文章介绍的 trusted setup 。

$l_1(x)$ 、$l_3(x)$ 这种变量多项式虽然是 prover 生成的，但我们依然可以使用一个 trusted setup 过程，对这些变量多项式提前进行加密。然后 prover 在产生 proof 的过程中，直接使用这些加密后得到的值。由于使用的加密后的值，并且还有 $\alpha$ 约束，prover 当然就只能使用变量多项式构造最终的多项式 $L(x)$ 、$R(x)$ 和 $O(x)$ 了。

拿上面的例子来说，prover 产生 $l_1(x)$、$l_3(x)$ 后，并不直接用于 prove 的过程，而是先将其进行加密，计算出 $g^{l_1(s)}$ 和 $g^{l_3(s)}$ 和 $g^{\alpha{l_1(s)}}$ 和 $g^{\alpha{l_3(s)}}$ 。这样一来在 prove 过程中，prover 也无法改变 $g^{l_1(s)}$ 和 $g^{l_3(s)}$ 的值，只能乖乖计算 ${(g^{l_1(s)})}^{a_1}$ 即 $g^{a_1l_1(s)}$ 。

2. 通用的转换

我们前面的所有的转换，其实都是限制比较多的，主要有：

1. 每个变量（$a_1$、 $b_1$ 等）的系数都为 1 ，没有其它值
2. 每个变量所在的位置只是一个变量，不能是一个运算组合
3. 只表示了乘法的转换，没涉及到加减除法

例如，如果我们运算等式为 $(3a_1 - 2b_2) \times b_1 = 3c_1 + 2$ ，目前为止我们是无法进行处理的。但如果只能处理前面的简单的转换，那零知识证明的可应用范围就太小了。幸运的是，我们可以处理这种情况。

下面这几段可能会让你看晕，不过请尽量硬着头皮看完，因为这是最宽泛的「一般情况」的介绍。后面我们会举一个具体的例子，就比较好理解了。

从 $(3a_1 - 2b_2) \times b_1 = 3c_1 + 2$ 这个例子可以看到，如果是乘法，那乘法两侧、等号右侧都不一定是单个变量，可能是多个变量之间的加减运算组合（但不能是乘除，一会我们再说）；变量的系数也可能是任意值。让我们用一个可以概括这种情况的、更加宽泛的等式来「定义」这种情况。假设我们一共有 $n$ 个变量 $v_i, i \in { {0…n}}$ ；有 $d$ 个这样的运算组合，所以我们有 ：

其中系数 $c_{d,l_i}$ 、$c_{d,r_i}$ 和 $c_{d,o_i}$ 可以是任意值，正数负数都可以（负数时表示减法运算）。不要被这一堆算式吓到，我们只要将更一般的情况用更一般的表示方法表示出来而已。

上面 ${(a)}$ 这一组等式，实际上代表的是一种对变量 $v_i$ 的约束。所谓约束，就是无论 $v_i$ 取什么值，一定要满足 $(a)$ 里面所有等式才行。这样一组等式的术语叫做 rank 1 constraint system ，即 R1CS ，翻译成中文为 秩为 1 的约束系统。秩 是线性代数里的概念，但这里我们并没有用矩阵的方式来表示 r1cs ，但正式的论文以及 v 神的文章，都是用矩阵来表示的。但用矩阵表示更抽象，我们这里先用这种更容易懂的方式。本篇文章的最后我们会再用矩阵的方式解释一遍。

所有的变量 $v_i$ 组成的集合，就是叫 witness

那这种情况下，我们应该怎么进行转换呢？其实方法都是一样的。我们依然为每个变量 $v_i$ 定义一个变量多项式 $l_i(x)$ 、$r_i(x)$ 和 $o_i(x)$ 。因为我们有 $n$ 个变量，所以有 $n$ 个 $l$ 多项式（同样 $r$ 和 $o$ 多项式也是 $n$ 个），所以：

所有的变量多项式，如 $l_1(x), r_1(x), o_1(x)$ 等，再加上 $t(x)$ ，这些多项式组成的集合，术语叫做 QAP（quadratic arithmetic program）。

我们依然取从 $1$ 到 $d$ 这样 $d$ 个点，让每个变量多项式经过这 $d$ 个点，并让变量多项式在某个点的值正好是变量的系数（如果系数是 0 ，代表没用到这个变量）：

可以看到，当 $x=1$ 时，$L(1) = v_1l_1(1) + v_2l_2(1) + … + v_nl_n(1)$ 恰好等于 $v_1c_{1,l_1} + v_2c_{1,l_2} + … + v_nc_{1,l_n}$ ，即 $\sum_\limits{i=1}^nc_{1,l_i}v_i$ 。其它值也类似的。

上面这段可能会让你看得头晕。没关系，我们下面看一个具体的例子，再结合上面一般情况的介绍，就会更清楚了。

2.1 例子

上一篇文章里，我们使用了下面一段代码作了开头：

fn foo(w: bool, a: i32, b: i32) -> i32 {
	if w {
		return a * b
	} else {
		return a + b
	}
}

数学的表达方式是：

我们就来看看如何把这个函数转换成多项式。

首先我们令变量 $v = f(w, a, b)$ ，然后把函数简化一下：

最终我们得到了 $w \times (a \times b - a - b) = v - a - b$ 。我们引入一个新的变量 $m$ ，令 $m = a \times b$ ；然后我们就可以把它拆成多个 $l \times r = o$ 的形式：

另外，由于原代码是 $w$ 是一个 bool 值，要么为 0 要么为 1 ，所以我们对 $w$ 的取值也要作限制：

我们得到了 3 个 $l \times r = o$ 这种形式的算式，其中有 5 个变量，所以我们现在可以知道，我们将产生 5 个变量多项式，最终得到一个最高阶为 2 的多项式。

这里等式 $(1)$ 、$(2)$ 和 $(3)$ 就是 r1cs ; $a$ 、$b$ 、$m$ 、$w$ 和 $v$ 就是 witness.

现在我们要写出来我们的 $L(x)$ 、 $R(x)$ 和 $O(x)$ ：

可以看到组装 $L$ 、$R$ 、$O$ 非常简单，你只要无脑将所有变量乘上对应的变量多项式，然后将它们加在一起就行了。只不过为了方便，这里我们调整了一下位置（其实是每个变量在等式 $(1)$ $(2)$ $(3)$ 中出现的顺序）。

接下来我们就要选择变量多项式经过的点以及它们的值了。由于有 3 个 $l \times r = o$ 这样的算式，我们需要随便取 3 个点，假设是 ${ {1, 2, 3}}$ 这三个点。我们要求：

1. 当 $x=1$ 时，$L(1) \times R(1) = O(1)$ 等于等式 $(1)$
2. 当 $x=2$ 时，$L(2) \times R(2) = O(2)$ 等于等式 $(2)$
3. 当 $x=3$ 时，$L(3) \times R(3) = O(3)$ 等于等式 $(3)$ 所以我们可以让 $x=1$ 时，每个 $l(1)$ 就是等式 $(1)$ 中 $\times$ 号左侧的变量的系数；每个 $r(1)$ 就是等式 $(1)$ 中 $\times$ 号右侧的变量的系数；每个 $o(1)$ 就是等式 $(1)$ 中 $=$ 号右侧的变量的系数。$x=2$ 时就是对应的等式 $(2)$ 中的变量的系数；$x=3$ 时也类似：

如此定义以后，你会发现，当 $x=1$ 时：

嗯，恰好等于等式 $(1)$ ，即 $1 \cdot a \times 1 \cdot b = 1 \cdot m$ 。$x=2$ 时代入也恰好可以算出等式 $(2)$，$x=3$ 时代入也恰好可以算出等式 $(3)$ ，这里就不一一列举了。

有了 $(\textrm{I})$ 、$(\textrm{II})$ 和 $(\textrm{III})$ 中对各个变量多项式在 $x = {1, 2, 3}$ 三个点的取值定义， 我们就可以通过快速傅利叶变换（或简单的解方程，手算就可以）的方式，求解出各变量多项式了。某些变量多项式（如 $(\textrm{I})$ $(\textrm{II})$ $(\textrm{III})$ 中没有下划线的变量多项式）在 ${1, 2, 3}$ 三个点时取值都是 0 ，所以我们可以知道这些多项式就是与 $x$ 轴重合的一条直线（如 $l_b(x) = 0$），所以我们在生成 $L(x)$ 、$R(x)$ 和 $O(x)$ 时干脆就不用它们，也就是上面对 $L(x)$ 、$R(x)$ 和 $O(x)$ 定义时可以去掉没有下划线的部分：

最终我们得到各变量多项式为：

所以当 prover 知道了 ${a, b, m, w, v}$ 这些变量的值时，ta 就可以算出真正的 $L(x)$ 、$R(x)$ 和 $O(x)$ 这三个多项式了。

2.2 乘法以外的转换

前面我们只涉及到了 $l \times r = o$ 这样的乘法，但计算中也有加、减、除，该怎么办呢？其实加减除都是可以转换成乘法的：

注意这里我们引入了一个常数 1 ，但我们要求 $\times$ 两侧必须是 $\sum_\limits{i=1}^{n}c_{1,r_i}v_i$ 这样的形式，所以我们把 1 改成 $1 \cdot v_{one}$ ，这里的 1 代表参数 $c_{1,r_i}$ ，$v_{one}$ 则是一个新增的变量，它的取值只能是 1 ，所以我们必须加一个限制：$v_{one} \times v_{one} = v_{one}$ ，但这也只能限制 $v_{one}$ 取值 1 或 0 ，不能限制只是 1 （这种情况下，$v_{one}$ 在变量中的位置是固定的并且是公开的，也就是所谓的 public input；verifier 会把 $v_{one}$ 设置成 1 后去验证，从而保证 $v_{one}$ 的值确实是 1 ）。

2.3 为什么只能有加减

你可能已经注意到，我们前面介绍的时候，用的是连加符，即 $\sum$ ，也就是说 $\times$ 两侧的算式里，可以有加和减（当 $c$ 为负数时就是减），不能有乘法（更不能有除法）。这是为什么呢？

还记得前面我们在生成 proof 的时候，prover 是要计算 $g^{L(s)}$ 的，也即 ${(g^{l_a(s)})}^a \cdot {g^{l_w(s)}}^w$ ，并且 $g^l$ 基本是作为一个整体提供给 prover。如果 $L(x)$ 里出现乘法，如 $L(x)=al_a(x) \cdot wl_w(x)$ ，那么 $g^{L(s)} = g^{al_a(s) \cdot wl_w(s)} = {(g^{al_a(s)})}^{wl_w(s)}$ ，但 trusted setup 能提供的只有 $g^{l_w(s)}$ ，不能提供 $l_w(s)$，所以这样是无法计算的。所以 $\times$ 两侧和 $=$ 右侧只能有加减，不能有乘除。

3. 新的证明过程

下面过程中， $n$ 始终为变量的数量（即 witness 数量）；$d$ 始终为约束的数量（即 r1cs 中等式的数量）

common setup:

1. 多方参与 trusted setup ，得到 $(g^{\alpha}, g^{s^i}, g^{ {\alpha}s^i})$ ，其中 $i$ 的最大值足够大，一般远超过 r1cs 中的等式数量 $d$ 。

生成 r1cs 和 QAP:

1. prover 根据具体问题，生成 r1cs .
2. prover 根据 r1cs 生成 QAP: $l_i(x)$、$r_i(x)$ 、$o_i(x)$ , $i \in {1,2..,n}$ ，其中 $n$ 为变量的个数 ；假设 r1cs 中有 $d$ 个等式（即约束数量为 $d$ ），所以可以令 $t(x) = (1-x)(2-x)…(d-x)$

QAP setup:

1. prover 使用 common setup 中生成的值 ，分别计算 $g^{l_i(s)}$ 、$g^{r_i(s)}$ 、$g^{o_i(s)}$ 、$g^{ {\alpha}l_i(s)}$ 、$g^{ {\alpha}r_i(s)}$ 、$g^{ {\alpha}o_i(s)}$ ，$i \in {1,2…,n}$
2. 在上一步的基础上，再次多方参与 trusted setup ，加密 $g$ 、 $g^{\alpha}$ 、$g^{t(s)}$ 、 $g^{l_i(s)}$ 、$g^{r_i(s)}$ 、$g^{o_i(s)}$ 、$g^{ {\alpha}l_i(s)}$ 、$g^{ {\alpha}r_i(s)}$ 、$g^{ {\alpha}o_i(s)}$ ，$i \in {1,2…,n}$ 。得到 $g^{s’}$ 、 $g^{\alpha{\alpha}’}$ 、$g^{s’t(s)}$、 $g^{s’l_i(s)}$ 、$g^{s’r_i(s)}$ 、$g^{s’o_i(s)}$ 、$g^{ {\alpha}’s’{\alpha}l_i(s)}$ 、$g^{ {\alpha}’s’{\alpha}r_i(s)}$ 、$g^{ {\alpha}’s’{\alpha}o_i(s)}$ ，$i \in {1,2,…,n}$ 。（回想前面文章介绍的 setup 过程，这里 $s’$ 和 $\alpha’$ 其实相当于所有参与 setup 的人生成的 $s$ 和 $\alpha$ 分别相乘后的值）（这里列举的值在最终版本里可能都不存在了，但目前我们只理解到这里，也就先这样写了）
3. 最终得到 ：
   • proving key: ${g^{s’},g^{ {\alpha}’s’},g^{s’l_i(s)},g^{s’r_i(s)},g^{s’o_i(s)},g^{ {\alpha}’s’{\alpha}l_i(s)},g^{ {\alpha}’s’{\alpha}r_i(s)},g^{ {\alpha}’s’{\alpha}o_i(s)}}, i \in {1,2,…,n}$
   • verification key: ${g, g^{\alpha}, g^{\alpha{\alpha}’}, g^{s’}, g^{s’t(s)}}$

prover:

1. 得到 witness 的具体取值（即每个 $v_i$ 的值）
2. 使用 proving key 中的值，计算：
   \(\begin{align} {(g^{s'l_1(s)})}^{v_1} \cdot {(g^{s'l_2(s)})}^{v_2}...{(g^{s'l_n(s)})}^{v_n} &= g^{v_1s'l_1(s)+v_2s'l_2(s)+...+v_ns'l_n(s)} = g^{s'L(s)} = E_L\\ {(g^{s'r_1(s)})}^{v_1} \cdot {(g^{s'r_2(s)})}^{v_2}...{(g^{s'r_n(s)})}^{v_n} &= g^{v_1s'r_1(s)+v_2s'r_2(s)+...+v_ns'r_n(s)} = g^{s'R(s)} = E_R\\ {(g^{s'o_1(s)})}^{v_1} \cdot {(g^{s'o_2(s)})}^{v_2}...{(g^{s'o_n(s)})}^{v_n} &= g^{v_1s'o_1(s)+v_2s'o_2(s)+...+v_ns'o_n(s)} = g^{s'O(s)} = E_O \\ \end{align}\)
3. 同样使用 proving key 中的值计算：
   \(\begin{align} {(g^{ {\alpha}'s'{\alpha}l_1(s)})}^{v_1}\cdot{(g^{ {\alpha}'s'{\alpha}l_2(s)})}^{v_2}...{(g^{ {\alpha}'s'{\alpha}l_n(s)})}^{v_n} &= g^{ {\alpha}'s'{\alpha}v_1l_1(s)+{\alpha}'s'{\alpha}v_2l_2(s)+...+{\alpha}'s'{\alpha}v_nl_n(s)} = {(g^{ {\alpha}'s'L(s)})}^{\alpha} = E_{L'}\\ {(g^{ {\alpha}'s'{\alpha}r_1(s)})}^{v_1}\cdot{(g^{ {\alpha}'s'{\alpha}r_2(s)})}^{v_2}...{(g^{ {\alpha}'s'{\alpha}r_n(s)})}^{v_n} &= g^{ {\alpha}'s'{\alpha}v_1r_1(s)+{\alpha}'s'{\alpha}v_2r_2(s)+...+{\alpha}'s'{\alpha}v_nr_n(s)} = {(g^{ {\alpha}'s'R(s)})}^{\alpha} = E_{R'}\\ {(g^{ {\alpha}'s'{\alpha}o_1(s)})}^{v_1}\cdot{(g^{ {\alpha}'s'{\alpha}o_2(s)})}^{v_2}...{(g^{ {\alpha}'s'{\alpha}o_n(s)})}^{v_n} &= g^{ {\alpha}'s'{\alpha}v_1o_1(s)+{\alpha}'s'{\alpha}v_2o_2(s)+...+{\alpha}'s'{\alpha}v_no_n(s)} = {(g^{ {\alpha}'s'O(s)})}^{\alpha} = E_{O'}\\ \end{align}\)
4. 计算 $h(x) = \frac{L(x) \times R(x)-O(x)}{t(x)}$ （由于 $L(x)$ 、$R(x)$ 、$O(x)$ 和 $t(x)$ 都是 prover 生成的，prover 当然可以计算出 $h(x)$ 。但要注意的是，还记得前面生成 $L(x)$ 、$R(x)$ 和 $O(x)$ 时都要用到 witness 即 $v_i$ 的值，所以 prover 只有在拿到具体的 witness 值以后才能计算出 $h(x)$ ，而无法像之前我们文章里介绍的那样，提前计算好）
5. 得出 $h(x)$ 后，使用 common setup 中的值计算 $g^{h(s)}$ ，然后利用 proving key 中的值计算：
   \(\begin{align} {(g^{s'})}^{h(s)} = g^{s'h(s)} = E_h \\ {(g^{ {\alpha}'s'})}^{h(s)} = g^{ {\alpha}'s'h(s)} = E_{h'} \\ \end{align}\)
6. 取随机数 $\delta$ ，分别加密 ${E_L, E’_L, E_R, E’_R, E_O, E’_O, E_h, E’_h}$：
   \(\begin{align} E'_L&={(E_L)}^\delta\\ E'_{L'}&={(E_{L'})}^\delta\\ E'_R&={(E_R)}^\delta\\ E'_{R'}&={(E_{R'})}^\delta\\ E'_O&={(E_O)}^{ {\delta}^2}\\ E'_{O'}&={(E_{O'})}^{ {\delta}^2}\\ E'_h&={(E_h)}^{ {\delta}^2}\\ E'_{h'}&={(E_{h'})}^{ {\delta}^2}\\ \end{align}\)
7. 将计算得出的值 \(({E'_L}, E'_{L'}, E'_R, E'_{R'}, E'_O, E'_{O'}, E'_h, E'_{h'})\) 传回给 verifier.

verifier: 使用 verification key 进行如下验证：

1. 验证 \(e(E'_L, g^{\alpha{\alpha}'})=e(E'_{L'}, g)\), 即 $e({(g^{s’L})}^{\delta}, g^{\alpha{\alpha}’})=e({({(g^{ {\alpha}’s’L})}^{\alpha})}^{\delta}, g)$ （它们都等于 $e(g,g)^{ {\alpha}{\alpha}’s’L{\delta}}$）
2. 验证 \(e(E'_R, g^{\alpha{\alpha}'})=e(E'_{R'}, g)\), 即 $e({(g^{s’R})}^{\delta}, g^{\alpha{\alpha}’})=e({({(g^{ {\alpha}’s’R})}^{\alpha})}^{\delta}, g)$ （它们都等于 $e(g,g)^{ {\alpha}{\alpha}’s’R{\delta}}$）
3. 验证 \(e(E'_O, g^{\alpha{\alpha}'})=e(E'_{O'}, g)\), 即 $e({(g^{s’O})}^{ {\delta}^2}, g^{\alpha{\alpha}’})=e({({(g^{ {\alpha}’s’O})}^{\alpha})}^{ {\delta}^2}, g)$ （它们都等于 $e(g,g)^{ {\alpha}{\alpha}’s’O{ {\delta}^2}}$）
4. 验证 \(e(E'_h, g^{ {\alpha}'})=e(E'_{h'},g)\)，即 $e({(g^{s’h})}^{ {\delta}^2}, g^{ {\alpha}’})=e({(g^{ {\alpha}’s’h})}^{ {\delta}^2}, g)$，（它们都等于 $e(g,g)^{ {\alpha}’s’h{ {\delta}^2}}$）
5. 验证 \(e(E'_L,E'_R)=e(E'_O,g^{s'}){\cdot}e(E'_h,g^{s't})\)，即 $e({(g^{s’L})}^{\delta},{(g^{s’R})}^{\delta})=e({(g^{s’O})}^{ {\delta}^2},g^{s’}){\cdot}e({(g^{s’h})}^{ {\delta}^2}, g^{s’t})$ ，即 $e(g,g)^{LR(s’)^2{\delta}{\delta}}=e(g,g)^{(s’)^2O{ {\delta}^2}}{\cdot}e(g,g)^{(s’)^2ht{ {\delta}^2}}=e(g,g)^{(O+ht)(s’)^2{ {\delta}^2}}$

4. 总结

这篇文章里，我们对多项式转换作了改进，主要包括两方面：一是约束了同一个变量在不同约束中的取值必须一样，这是通过引进变量多项式实现的；二是处理了更一般的情况，包括除乘法外的加减除。因此整个逻辑和计算过程变得更复杂了，但其实万变不离其宗，复杂只是表现在形式上，核心逻辑变化很少。

5. 附：矩阵的表示形式

在上面的介绍中，我们使用了如下的表示形式：

这种方式比较直观，更容易理解，但也显得啰嗦。其实大多数的资料里，都会使用矩阵的表示方式，这种方式更简洁。为了能在学习其它资料时可以看得懂矩阵的表示形式，我们这里再把由约束到多项式之间的推理过程再用矩阵演示一遍。

为了方便，我们把上面的约束重新写一下：

我们需要先用向量 $\vec{s} = [a, b, m, w, v]$ 来表示 witness 。然后我们需要找出一批向量 ${\vec{l}_i, \vec{r}_i, \vec{o}_i}, i \in {1, 2, 3}$ ，使得 $\vec{l}_i \cdot \vec{s} \times \vec{r}_i \cdot \vec{s} = \vec{o}_i \cdot \vec{s}, i \in {1, 2, 3}$ 能分别代表上面第一个约束和第二个约束。我们一个一个来看。当 $i = 1$ 时，我们可以令：

所以有：

可以看到 $\vec{l}_1 \cdot \vec{s} \times \vec{r}_1 \cdot \vec{s} = \vec{o}_1 \cdot \vec{s}$ 正好可以等价于第一个约束。 当 $i=2$ 时，我们令：

所以有：

可以看到 $\vec{l}_2 \cdot \vec{s} \times \vec{r}_2 \cdot \vec{s} = \vec{o}_2 \cdot \vec{s}$ 正好可以等价于第二个约束。

类似的，当 $i = 3$ 时我们令：

也可以得到 $\vec{l}_3 \cdot \vec{s} \times \vec{r}_3 \cdot \vec{s} = \vec{o}_3 \cdot \vec{s}$ 正好与第三个约束等价。

小结一下，目前我们得到了：

使得将它们分别与 $\vec{s}$ 相等时，正好可以等约前面的约束。

然后我们将所有的 $\vec{l}_i$ 放在一起，同样的将 $\vec{r}_i$ 和 $\vec{o}_i$ 也分别放在一起，得到：

可以看到这个过程与前们我们使用非矩阵的表示形式的本质是一样，只不过换了种表达方式：前面我们到这一步时，得到的是：

这个多项式的表示方式与上面向量矩阵的表示方式完全一样（但注意上面等式相同位置的值可能上面矩阵中相同位置的值意义不一样，比如上面 $(\textrm{I})$ 中的第 2 行里的 1 代表的是 $w$ 的值，与之对应的是上面矩阵中 $L$ 的第 2 个向量的第 4 个值，而非第 2 个 ）.

接下来，按照我们之前介绍的逻辑，我们要分别求解变量多项式。在矩阵中，第一个向量矩阵中的每列，对应着 witness 中同一变量。比如对于向量矩阵 $O$ 来说：

第一列 \(\begin{bmatrix}0\\-1\\0\end{bmatrix}\) 对应着 $\vec{s}$ 中的 $a$ ；第二列 \(\begin{bmatrix}0\\1\\0\end{bmatrix}\) 对应着 $\vec{s}$ 中的 b 。其它列是类似的。而求解变量多项式方法与前面是一样的。比如对于 $O$ 中的第一列，对应前我们之前介绍的变量多项式 $o_a(x)$ ，我们令 $o_a(x)$ 经过 $(1, 0), (2, -1), (3, 0)$ 这三个点，使用快速傅利叶变换等方法，得到多项式：

下面这个图可以说明这个变化过程：

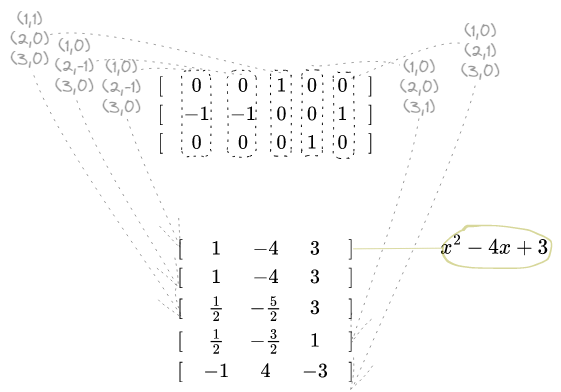
注意图中下半部分的向量矩阵中每个向量代表一个多项式参数，从左到右对应的 $x$ 的幂是降低的。

$L$ 和 $R$ 类似， 所以最终得到的多项式也使用矩阵的方式表示：

上面的过程我们只需要计算一次就可以。等拿到真正的 witness 值（即 $a$ 、$b$ 等不再是个变量名，而是具体的值的时候），再使用$\vec{s}$ 分别乘以上面三个向量矩阵，就可以得到最终的 $L(x)$ 、$R(x)$ 和 $O(x)$ ：

可以看到，最终 $L(x)=al_a(x)+wl_w(x)$ ，$R(x)$ 和 $O(x)$ 也类似，这与我们前面使用非矩阵形式得到的结果是一样的。

以上就是矩阵形式的表达方式，它更简洁、更抽象，但也更难理解些（其实关键是记住了矩阵行与列的含义）。