为什么叫“重识概率”
之前的文章说过，大学里的数学不能说白学了，但也不好意思跟别人说自己学过。而概率论是我大学里唯一挂掉的一科。不过原因之一是因为遇到院系里的四大名捕老师之一（隐约记得有三分之二的同学都挂了）。
但是点背不能怨社会，之所以没学好概率，说到底是自己心里的“不认同”。我始终觉得概率是一个很虚的东西，对于某件事来说，发生了就是发生了，没发生就是没发生。即使你计算出不发生的概率是99%，但仍有1%的机会事情就真的发生了，那你得到的概率值还有什么意义呢？
但是工作了以后越来越发现，机器学习这些领域用得最多的还就是我唯一挂掉的这一科，我也是醉了。被逼无奈我只能重新思考自己的想法，既然世界上有这么多研究和应用，很可能他们是对的，我的想法是错的（是的，这个问题其实就应用了概率，我猜测别人大概率是对的，而我大概率是错的）。所以我开始逼自己重新去思考和学习概率。此所谓重识之一吧。
在学习的过程中，我遇到了《程序员的数学》这个系列的书，并认为非常适合当前阶段的我。作者在书中开头就提到“概率的难点在于它不够直观”，我深以为然。接着作者就提出了“上帝视角”这种方法来理解概率，让我觉得“概率还可以这样理解”和“概率本来就应该这样理解”。此所谓重识之二。
说点题外话。我大学里对概率的不认同，其实是基于“当事人”这个身份来对概率进行思考，而别人是以“旁观者”的身份来学习概率的。不同点显而易见，比如新闻报道新生儿死亡率是0.1%，而作为一个即将成为父母的成人，会去关心是0.1%还是0.2%吗？他只会关心自己的孩子是不是健康。而对于统计局或某些相关单位的人来说，0.1%还是0.2%是它们密切关注的。从这个角度看，概率统计其实非常残酷。
什么是上帝视角
上帝视角是一种看待这个世界的角度。从上帝视角来看，宇宙中存在着多个平行世界。对于每个世界来说，根本没有概率问题，所有事件都是在按照既定的剧本在进行（芸芸众生的生活都是你给他们编排好的）。
这么说有点玄乎，我们换一种接地气的方法。对于某一事件，我们安排足够多的会场，可以完整演示事件的所有情况。注意会场中真的就是演示：会场中的事件怎么进行是有剧本的，所有事件的进展都按设定的剧本进行，不可更改。那么对于这一事件的某一种情况的概率，我们只要数一下按这种情况进行演示的会场数量，占总会场的比例就可以了。
我们通过一个简单的例子来体会一下这种方法。我们都知道掷骰子时每个点的概率都是1/6，怎么用这种上帝视角来验证呢？我们安排12个会场（其实6个就可以恰好完整演示事件的所有情况，12个当然也可以），因为总共有6种情况，所以把所有的会场分成6组，每组两个。第一组两个会场只能掷出点数1 ，第二组只能掷出点数2，以此类推（此所谓写好的剧本）。如下面所示：
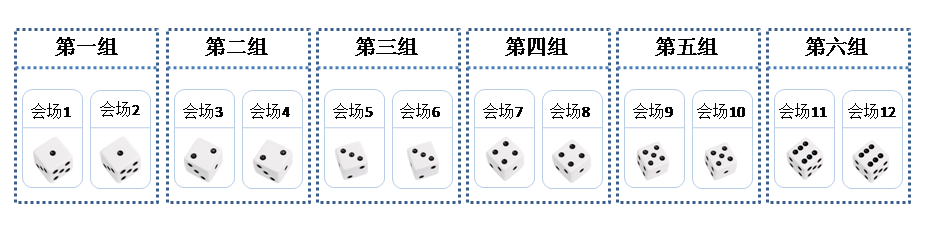可以看到总共有12个会场，掷出点数1的会场有两个，所以掷出点数1的概率为2/12 = 1/6。其它点数同理也是1/6。
你可能会说这也太小儿科了吧。
我们接下来看一个复杂一点的问题：蒙提霍尔问题。假设有三道门，其中一道门后面是一辆汽车，另两道门后面是山羊。作为挑战者需要尽可能猜中汽车，把汽车抱回家。裁判整个过程都明确知道每道门的后面是什么。开始时，挑战者选一道他认为后面是汽车的门，然后裁判会随机打开剩余两道门中是山羊的其中一道。这时挑战者有改变初选的机会。问题是挑战者应当坚持当初的选择还是改选另一道门？哪种做法猜中汽车的概率更大呢？
这个问题其实有些反直觉。对于我来说，一开始我觉得不管是否改选，选中的概率难道不应该都是1/2吗？因为裁判已经打开了一道没有汽车的门，根据规则，剩余两道门必然一个有汽车，一个有山羊。
我的这个直觉是错的。
我们用上帝视角来看一下这个问题。我们把会场分成3组，第一组所有会场的门1后面是汽车；第二组所有会场的门2后面是汽车；第三组所有会场的门3后面是汽车。在每一组中，又分成了三个小组分别演示挑战者初次选门1、门2、门3的情况。如下图所示：
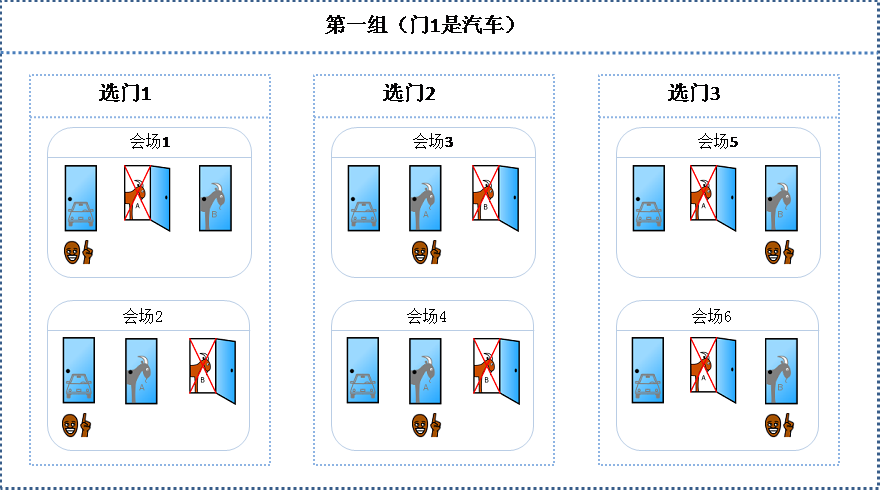
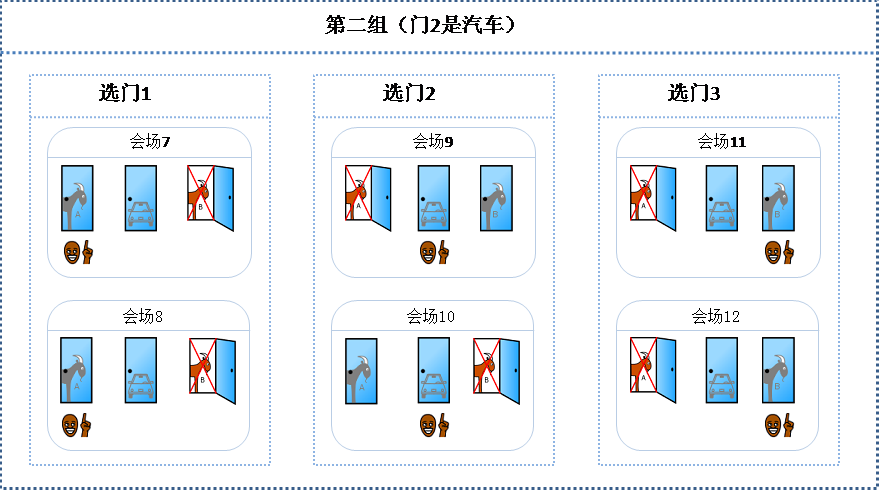
从图中可以看出，会场总数为18。如果挑战者在裁判打开一道门后仍坚持最初的选择，那么将有6个会场中的挑战者猜中汽车（会场1，2，9，10，17，18），比例为1/3；相反如果挑战者改变最初的选择，那么将有12个会场中的挑战者猜中汽车（会场3，4，5，6，7，8，11，12，13，14，15，16），比例为2/3。所以我们可以下结论说：如果挑战者在裁判打开一道门后改变最初的选择，选中汽车的机率为2/3，改选的做法猜中汽车的机率更大。
为什么我一开始的直觉是错的呢？因为我在作第二次选择时忽略了第一次选择的影响，而这两次选择之间不是独立的，第一次的选择会影响第二次选择的正确性。具体来说，如果我第一次选对了门，第二次改选必定选错；如果我第一次选错了门，第二次改选必定选对。但第一次选错的概率为2/3，大于第一次选对的概率，所以总体来看第二次改选选对的概率更大。
从这个例子可以看出，上帝视角把一个抽象的概率问题具体化了，因而可以使我们更直观的感受概率统计（这里真的是统计，我们只需要数一下会场数量就可以了）。所有离散的概率问题（事件可列举），都可以使用上帝视角来理解。
上帝视角的关键一点是演示各种情况的会场的数量。仔细观察上面演示蒙提霍尔问题的示例图可以发现，会场3与4进行了相同的演示（同样情况还有会场5与6、7与8、11与12、13与14、15与16），这其实是同一种情况，为什么要用两个会场来演示呢？我认为是因为本来其实是有两种情况的，只是限于规则裁判只能这样做，所以从结果上看就是进行了一样的演示。实际上许多问题都会出现由于规则限制等问题，多种不同选择的会场出现同一演示结果。如果将这些会场合并成一个，会使结果截然不同。
概率与面积
另一个将抽象概率具体化的方法是使用图形面积来表示。比如有个机灵的小朋友想出了一种方法可以判断带壳的花生里面的花生仁是否是坏掉的，但有1/4的机率误判。现在有10个花生，其中有3个是坏的。从中随机选一个，小朋友判断为坏花生的机率是多大呢？
我们使用一个长方形代表所有的可能性，其面积为1。由于10个花生中有3个是坏的，所以代表坏花生的面积是3/10，好花生的面积是7/10。如下图所示：
由于小朋友有1/4的误判率，所以在好花生的面积里，有1/4的面积被小朋友判断为坏花生；而在坏花生的面积里，有3/4的面积被判断为坏花生。如下图所示：
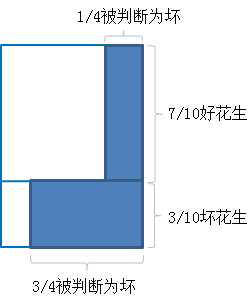
所以显而易见，图中被填充的部分的面积即为判断为坏花生的面积。所以小朋友判断为坏花生的面积为 $\frac{7}{10}\times\frac{1}{4} + \frac{3}{10}\times\frac{3}{4} = \frac{2}{5} = 0.4$
与把所有情况画出来相比，使用面积表示的方式更加简单。
总结
通过上帝视角这种方法，“概率”不再是个概率问题，而是众多世界里按上帝设计好的“剧本”进行演示而已。这个想法的确非常生动，让问题也更加易于理解。而上帝视角的关键，需要正确定义好会场的个数，否则出现多余或缺少的情况，都会影响最终的结果。
那么我们这个世界是否真的是众多平行世界中的一个呢？也许我们这个世界上发生的没发生的种种事件，只是像计算机程序一样，按照既定的代码在按部就班的执行而已？
参考资料：
- 程序员的数学2：概率统计