本篇文章分析的源码地址为:https://github.com/ethereum/go-ethereum
分支:master
commit id: 257bfff316e4efb8952fbeb67c91f86af579cb0a
引言
trie(Merkle Patricia Tree,又称MPT)是以太坊(ethereum)中用来加密存储任意(key,value)数据对的树形结构。它的插入、查找和删除效率都是O(log(N)),但它比其它树形结构如红黑树等更简单、更容易理解,并且还具有默克尔树的特性。我们期望从原理和源代码两方面入手,以期对其进行深入的了解。
我们分两篇来介绍trie。本篇是上篇,主要介绍相关原理。下篇会从源代码的角度入手对实现进行分析。
trie官方原理介绍在这里,下面原理部分的分析有不少是参考了官方的讲解文档。
trie原理
以太坊的Trie模块在普通Trie的基础上,进行了改进和优化。下面我们会首先介绍普通的Trie,然后看看以太坊对普通的Trie进行了哪些改进,以及在以太坊中的应用和特性。
预备知识:普通的Trie
关于什么是Trie,我觉得维基百科里的描述已经非常清楚了,大家可以先看看百科上的描述。这里我直接摘录部分我觉得重要的内容:
trie,又称前缀树或字典树,是一种有序树,用于保存关联数组,其中的键通常是字符串。与二叉查找树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。
特别注意字典树这个词,可以说是特别形象了。为什么呢?看完一个例子你就能理解了。
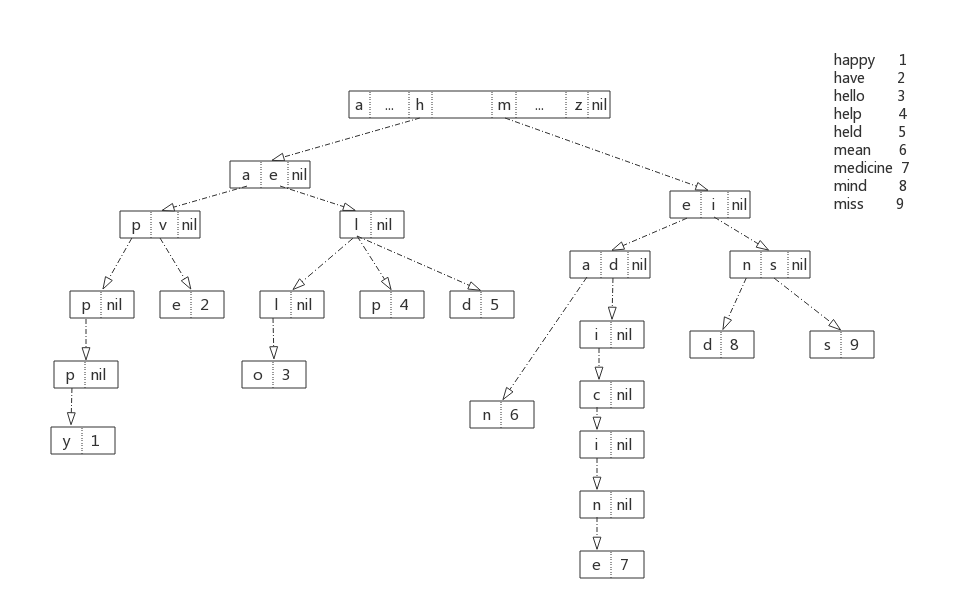 (图中每个结点都有一个类似于根结点那样的数组,但简单起见其它结点都把在这里无用的数组元素忽略了。)
(图中每个结点都有一个类似于根结点那样的数组,但简单起见其它结点都把在这里无用的数组元素忽略了。)
在上图中,每个结点其实都只是key的一部分,或者说就是key的一个字符。在按照某一个key向下遍历直到key最后一个字符时,也就找到了这个key对应的value。你有没有发现这种查找value的方式,跟查字典一模一样?所以说,字典树这个名字真的是非常形象。
虽然这里没有给出像样的定义,但看完维基百科和上面的例子,相信你已经可以理解什么是Trie了。一般来说,Trie的结点看上去是这样子的:
[ [Ia, Ib, … I*], value]
其中 [Ia, Ib, ... I*] 在本文中我们将其称为结点的 索引数组 ,它以key中的下一个字符为索引,每个元素I*指向对应的子结点。 value 则代表从根节点到当前结点的路径组成的key所对应的值。如果不存在这样一个key,则value的值为空。
以太坊trie的改动和优化
以上面描述的Trie为基础,以太坊主要从以下几个方面对其进行了改进和优化。
使用[]byte作为key的类型,而非字符串
在以太坊的Trie模块中,key和value都是[]byte类型。如果要使用其它类型,需要将其转换成[]byte类型(比如使用rlp进行转换)。当然这不是什么本质上改变,我个人感觉只是为了编码方便吧。因为rlp模块可以方便的把各种结构序列化成[]byte而不是string。
nibble: key类型的最小单位
你可能会疑惑,刚才不是说使用key的类型是[]byte吗?那最小单位自然是byte,nibble又是什么?
其实在以太坊的Trie模块对外提供的接口中,key类型当然是[]byte。但在内部实现里,将key中的每个字节按高4位和低4位拆分成了两个字节。比如你传入的key是:
[0x1a, 0x2b, 0x3c, 0x4d]
Trie内部将这个key拆分成:
[0x1, 0xa, 0x2, 0xb, 0x3, 0xc, 0x4, 0xd]
Trie内部的编码中将拆分后的每一个字节称为 nibble
但为什么要这样做呢?
如果使用一个完整的byte作为key的最小单位,那么前文提到的索引数组的大小应该是256(byte作为数组的索引,最大值为255,最小值为0)。而索引数组的每个元素都是一个32字节的哈希(这在下一条中进行了说明),这样每个结点要占用大量的空间。并且索引数组中的元素多数情况下是空的,不指向任何结点。因此这种实现方法占用大量空间而不使用。以太坊的改进方法,可以将索引数组的大小降为16(4个bit的最大值为0xF,最小值为0),因此大大减少空间的浪费。
使用hash引用结点而不是内存指针
在以太坊的实现中,索引数组的每个元素都是下一个结点的hash,而非指针。也就是说,父结点持有的是子结点的hash。
这种实现方式使得以太坊中的Trie带有了默克尔树的功能:如果两个Trie的根结点的hash相同,我们就可以断定,这两棵树的内容完全一样。Trie用来存储以太坊账户的状态(state)等,就是利用利用这个特性对区块进行校验的。
需要注意的是,这种实现也包括对value的引用。也就是说在以太坊的Trie中,遍历到叶子结点以后得到的是value的hash,而非value本身。使用这个hash从数据库中读取出来的值才是value。
当树的某条路径没有分支时,使用一个结点存储路径上的所有key
我们回看上面介绍字典树的那张图,其中”medicine”这条路径中,除了前三个字符’med’,其它字符都没有分支,因此为了节省空间,以太坊将这种情况下的结点缩减为一个。如下图所示:
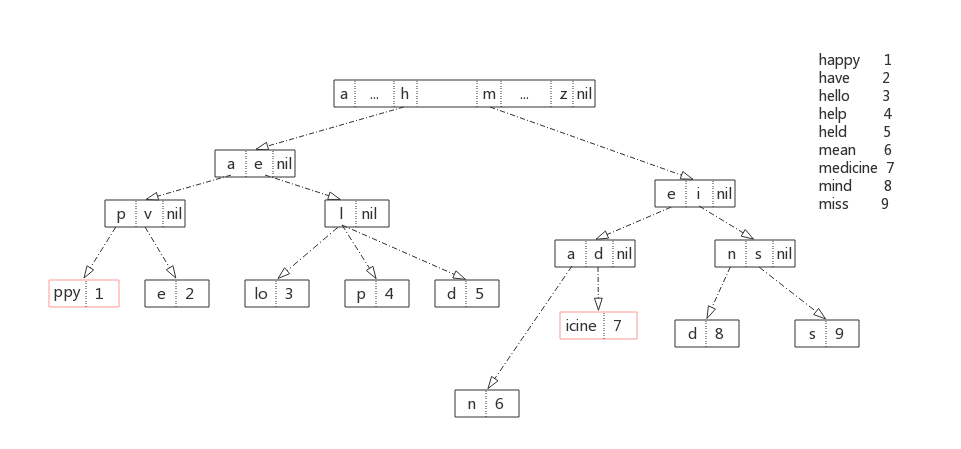
这样就可以进一步节省空间的开销。但同时也产生了一个问题:对于某个结点,如何知道它存储的是索引数组,还是key的数组呢?
以太坊解决这个问题的方式是通过结点元素个数的不同进行区分。以太坊在Trie内部将结点分成了两类:全节点(fullNode)和快捷节点(shortNode)。全节点有17个元素,而快捷结点有两个元素。它们的示意表达如下:
全结点: [i0, i2, … i15, value]
快捷结点: [ [k0, k1, … kn], value ]
可以看到全结点由索引数组(共16个元素)和一个value组成(前面说过value的引用也是通过hash,而不是直接存储value的值);而快捷结点有2个元素,一个是key数组,另一个就是value。
此时虽然可以知道一个结点存储的数据的格式,但对于快捷结点,仍有两个问题没有解决。 一个问题是,前面说过key的最小单位是nibble,。那么如果在快捷结点中nibble的个数是奇数,它重新组合成[]byte存储就会有麻烦。比如
nibbles: 0x1 0xa 0x2 0xb 0x3
组合成[]byte? 0x1a 0x2b 0x30 还是 0x01 0xa2 0xb3
可见无论怎么组合,都会有多写入一个无效的nibble。等再解析的时候,我们怎么知道哪个是无效的呢?
另一个问题是,我们该如何解析快捷结点中的value所代表的数据。它是代表真正的value数据,还是另一个结点?
这两个问题存在的原因在于,Trie中的结点是需要进行数据库存取的。如果只是在内存中,这两个问题不会存在:只在内存中没有必要把nibble组成的key变成[]byte类型;通过数据的结构体类型也很容易知道value所代表的数据类型。但要将快捷结点存入数据库中,需要将nibble组成的key变成[]byte存储(其实也可以直接存储nibble数组,只是多占了一倍空间);而从数据库中读取value所代表的数据时,需要知道是将其解析成一个新的结点,还是仅代表value原始值无需解析。
有问题就要解决。既然问题产生于数据库的存取,很自然地我们会想到,可以在存的时候加上一些信息,能标识出哪一位是无效的nibble,和value所代表的数据类型。当从数据库中取的时候,就可以根据这些信息将数据恢复啦。
是的,解决的思路都是类似的,只是实现方法千千万。以太坊的实现方法是在存入数据库时,将nibble组合成的[]byte值的第0个字节的高4位作为信息存储位而不存储真正的nibble字节。可以说这种方法真是一点内存都不浪费。
那么第0个字节的高4位是怎么组织的呢?目前我们有两个信息需要存储:
- nibble的个数的奇偶信息
- value代表结点还是真正的value数据
可以看到这俩个信息都是二元的(非此即彼),因此有2个bit就可以了。以太坊的做法是第0位存储奇偶信息,第1位存储value代表的类型。具体信息如下:
| hex char | bits | value代表类型 | nibble个数奇偶 | 低4位是否有效 |
|---|---|---|---|---|
| 0 | 0000 | 结点 | 偶数 | 无效 |
| 1 | 0001 | 结点 | 奇数 | 有效,第一个nibble |
| 2 | 0010 | 数据 | 偶数 | 无效 |
| 3 | 0011 | 数据 | 奇数 | 有效,第一个nibble |
可以看到当nibble个数为偶数时,第0个字节的低4位总是无效的;但为奇数时,低4位是有效的,其值为第一个nibble。
让我们通过例子来确认对这些描述的理解。以下示意的都是快捷结点:
[ [0xa, 0xb, 0xc, 0xd, 0xe], value_node ] // 奇数个nibble,value代表node
编码: 0x1a 0xbc 0xde
[ [0xa, 0xb, 0xc, 0xd], value_node ] //偶数个nibble,value代表node
编码: 0x00 0xab 0xcd
[ [0xa, 0xb, 0xc, 0xd, 0xe], value_data ] //奇数个nibble,value代表数据
编码: 0x3a 0xbc 0xde
[ [0xa, 0xb, 0xc, 0xd], value_data ] //偶数个nibble,value代表数据
编码: 0x20 0xab 0xcd
需要再强调一下的是,这个编码方法只有在数据库存取的时候才用到。在读到内存中以后,nibble是直接以[]byte类型存储的(虽然每个byte的最大值是15),且如果value代表的是数据则在nibble数组的最后append值16(注意16是一个无效的nibble值,因此可以和正常的nibble值作区分),代码中根据最后一个值是否是16判断value的类型。
另外虽然我们一直没有明确说明,但上面在说value代表的类型的时候,我们其实是在判断当前结点是不是叶子结点:如果是叶子结点,value当然代表数据;如果不是,value也当然代表一个node。
至此,所有问题都已解决,终于可以正常的将多个没有分支的结点压缩到一个结点存储了(为了解决一个问题,引入了好几个问题)。
我们来总结一下我们当前讨论的改进:以太坊通过以下方式,减少无分支路径上的结点数:
- 将结点类型分成了fullNode和shortNode,shortNode存储多个key的nibble
- 使用第0个字节的高4位编码,标识nibble的奇偶个数(也即第0个字节的低4位是否是有效的nibble)和value类型(也即当前结点是否是叶子结点)
内部节点引用计数
这一改进其实与trie原理本身没有关系,但我认为也是非常重要的,因此有必要在这里介绍一下。
在trie模块中,有一个Database对象,你可以理解为它是底层数据库的一个缓存层。在实际使用过程中,Trie对象就把Database作为数据库使用。但Database的重要功能不在于缓存,而在于缓存时对节点数据进行了引用计数,并提供了Database.Reference和Database.Dereference来引用和解引用某个trie节点。如果某个节点的引用计数变为0,则该节点将被从内存中删除,因而也不会被写入到真正的数据库中。
注意Database中只对内存中缓存的节点进行了引用计数,已经写入数据库的节点没有引用计数数据。
以太坊的trie模块为什么对trie作了这么一个改进呢?这主要是为了解决以太坊数据存储的问题。随着以太坊的长时间运行,以太坊数据已经非常大且仍在以类似指数的速度增长。增长的主要数据,就是以太坊的账户状态(state)信息,而以太坊trie作为state的底层数据组织方式,它的实现决定了这种增长速度。因为在以太坊中,每生成一个新的区块,不会直接修改上一个区块的state数据,而是类似于“写时复制”的机制,将数据修改后重新存储一份,对于trie来说则是生成新的子节点进行存储,如下图所示:
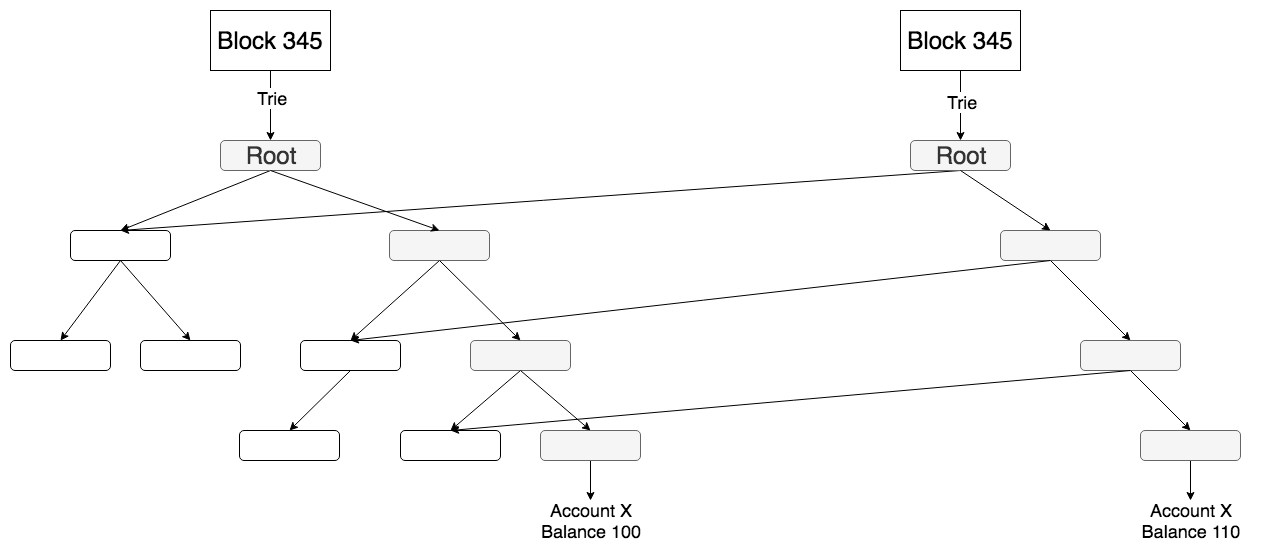
以上图为例,只要修改账户X的信息,就需要新增4个节点而不会修改原来的节点(实际情况可能不止4个),这就是state数据增长如此之快的原因。为了减轻数据存储的压力,以太坊提出了修剪区块(pruned block)的概念,即利用trie模块中的trie.Database对缓存节点进行引用计数,并在blockchain模块中进行相应的引用和解引用操作。如此释放了大量不需要保存的历史数据的存储空间。(关于区块修剪可以参考这里)
特性
从上面介绍的所有改进我们可以了解到,以太坊的实现非常节省内存。另一个重要的改进是,它与默克尔树进行了融合,在可以高效存取(key,value)对的同时,还具有默克尔树的特性:通过比较两个Trie对象的根结点的hash,就可以判断这两棵树是否存储了相同的内容。
默克尔树的这一特性是非常有用的。在以太坊中,Trie用来存储四种对象:
- State
- Storage
- Transactions
- Receipts
现在我们可以不必理会这些对象的意义(其实我现在也不是全部了解),但它们在Trie这一层面都是类似的,我们以State举例。以太坊的State存储了区块上所有账号的信息,包括账户余额等。这些账号信息随着区块的变化而变化。在即将打包一个新的区块时,以太坊会更新代表State的Trie对象,并将更新后的Trie根结点hash写入新的区块头中。当其它运行以太坊节点的机器收到这个区块时,它可以根据上一个区块中的State信息,加上新块区的变动后,将得到的Trie的根结点hash与区块头中的进行比较。如果hash一致,则这个区块的State信息就得到了承认。
总结
这篇文章里,我们主要介绍了以太坊中Trie的实现原理。以太坊对传统Trie进行了优化,使其可以更加的节省内存。更重要的是,它与默克尔树进与了融合,使其在应用时更加方便有效。当然这些改进和融合也引入了复杂度,正如前面说的,为了解决一个问题,引进了两个新的问题。这也是以太坊Trie的实现相对较复杂的主要原因。
下一篇中,我们将通过源代码的角度,对Trie进行进一步的分析。